सोडियम प्रकाश के लिए दो पीली रेखाएँ तरंगदैर्ध्य λ1 तथा λ2 आपतित होती हैं। यदि इन दोनों का माध्य 6000Å है तथा |λ2−λ1|=6Å है, तो इन λ1 तथा λ2 के संगत इन दोनों ऊर्जा स्तरों के मध्य लगभग अन्तर होगा
2×10−3eV
2eV
2000eV
2×10−6eV
The correct Answer is:A
दिया है, λ 38. (a) , और λ2 का माध्य =6000Å
|λ2−λ1|=6Å
अतः λ1+λ22=6000Å
λ1+λ2=12000Å ...(i)
λ1−λ2=6Å ...(ii)
समी (1) और समी (ii) का योग करने पर,
2λI=12006
λ2=120062=6003Å
और λ1=5997Å
ऊर्जा का अन्तर, ΔE=hcλ1=hcλ2
ΔE=hc(1λ1−1λ2)
ΔE=6.6×10−34×3×108×(1λ1−1λ2)
=6.6×10−34x3×108×6×10−105997×10−10×6003×10−10×1.6×10−19eV
=2.12×10−3eV≈2×10−3eV
Topper's Solved these Questions
Similar Questions
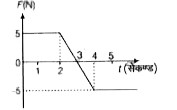
किग्रा द्रव्यमान का एक ब्लॉक x- अक्ष पर गतिमान है इस पर कार्यरत बल F चित्रनुसार है। समय t = 2 सेकण्ड पर ब्लॉक का वेग -3मी /से है , तो समय t = 4 सेकण्ड पर ब्लॉक की चाल क्या होगी ?
View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length lambda_(1) and lambda_(2) . If they collide and stick then the de-Broglie wave length of system after collision is : (A) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (B) lambda = (lambda_(1))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (C) lambda = (sqrt(lambda_(1)^(2) + lambda_(2)^(2)))/(lambda_(2)) (D) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1) + lambda_(2)))
View SolutionIf λ1andλ2 are the wavelength of the first members of the Lyman and Paschen series, respectively , then λ1λ2 is
View Solutionएक प्रकाशीय यंत्र में प्रयुक्त प्रकाश के तरंगदैर्घ्य λ1=4000Å और λ2=5000Å हैं। तब उनकी विभेदन क्षमताओं का अनुपात (λ1 और λ2 के संगत ) होगा -
View SolutionIf the matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent,
the value of λ21+λ22+λ23 is
View SolutionFor sodium light, the two yellow lines occur at lambda_(1) and lambda_(2) wavelengths. If the mean of these two is 6000Å and |lambda_(2)-lambda_(1)|=6Å , then the approximate energy difference between the two levels corresponding to lambda_(1) and lambda_(2) is
View SolutionIf λ1 and λ2 are the wavelengths of the first members of the Lyman and Paschen series respectively, then λ1:λ2 is
View SolutionIf λ1=andλ2 are the wavelengths of the first members of Lyman and Paschen series respectively, then λ1:λ2, is
View Solutionयदि λ1 तथा λ2 क्रमशः लाइमन और पाश्चन श्रेणी की प्रथम रेखाओं का तरंगदैर्ध्य हैं | तब λ1:λ2
View SolutionTwo particle are moving perpendicular to each with de-Broglie wave length lambda_(1) and lambda_(2) . If they collide and stick then the de-Broglie wave length of system after collision is : (A) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (B) lambda = (lambda_(1))/(sqrt(lambda_(1)^(2) + lambda_(2)^(2))) (C) lambda = (sqrt(lambda_(1)^(2) + lambda_(2)^(2)))/(lambda_(2)) (D) lambda = (lambda_(1) lambda_(2))/(sqrt(lambda_(1) + lambda_(2)))
View SolutionIf the characteristic wavelengths of the x-rays and the-rays respectively lambda_(1) " तथा " lambda_(2) Then there will be a relationship between them
View Solutionlambda_(1) and lambda_(2) are the wavelength of the first numbers of the Lyman and Paschen series respectively, then find lambda_(1): lambda_(2)
View SolutionIf , λ1 and λ2 are the wavelength of the numbers of the Lyman and Paschen seri respectively. Then λ1:λ2=.....
View SolutionIf the matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent,
the value of λ21+λ22+λ23 is
View SolutionIf lambda_(1) and lambda_(2) are the wavelength of the first members of the Lyman and Paschen series, respectively , then lambda_(1) :lambda_(2) is
View Solution
