If λ1andλ2 are the wavelength of the first members of the Lyman and Paschen series, respectively , then λ1:λ2 is
1:3
1:30
7:50
7:108
The correct Answer is:D
To solve the problem of finding the ratio of the wavelengths of the first members of the Lyman and Paschen series, we can follow these steps:
Step 1: Identify the transitions for the Lyman and Paschen series
- The Lyman series corresponds to transitions from higher energy levels to the first energy level (n=1). The first member of the Lyman series is the transition from n=2 to n=1.
- The Paschen series corresponds to transitions from higher energy levels to the third energy level (n=3). The first member of the Paschen series is the transition from n=4 to n=3.
Step 2: Use the Rydberg formula for wavelength
The Rydberg formula for the wavelength of light emitted during an electron transition is given by:
1λ=R(1n21−1n22)
where R is the Rydberg constant, n1 is the lower energy level, and n2 is the higher energy level.
Step 3: Calculate λ1 for the Lyman series
For the Lyman series (transition from n=2 to n=1):
- n1=1
- n2=2
Using the Rydberg formula:
1λ1=R(112−122)=R(1−14)=R(34)
Thus,
λ1=43R
Step 4: Calculate λ2 for the Paschen series
For the Paschen series (transition from n=4 to n=3):
- n1=3
- n2=4
Using the Rydberg formula:
1λ2=R(132−142)=R(19−116)
Finding a common denominator (144):
1λ2=R(16−9144)=R(7144)
Thus,
λ2=1447R
Step 5: Find the ratio λ1:λ2
Now we can find the ratio λ1:λ2:
λ1λ2=43R1447R=4⋅73⋅144=28432=7108
Final Result
Thus, the ratio of the wavelengths of the first members of the Lyman and Paschen series is:
λ1:λ2=7108
- The Lyman series corresponds to transitions from higher energy levels to the first energy level (n=1). The first member of the Lyman series is the transition from n=2 to n=1.
- The Paschen series corresponds to transitions from higher energy levels to the third energy level (n=3). The first member of the Paschen series is the transition from n=4 to n=3.
The Rydberg formula for the wavelength of light emitted during an electron transition is given by:
For the Lyman series (transition from n=2 to n=1):
- n1=1
- n2=2
For the Paschen series (transition from n=4 to n=3):
- n1=3
- n2=4
Now we can find the ratio λ1:λ2:
Thus, the ratio of the wavelengths of the first members of the Lyman and Paschen series is:
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Multiple Correct13videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Linked Comprehension62videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Subject17videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct10videos
ALTERNATING CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer5videos
CAPACITOR AND CAPACITANCE
Similar Questions
Knowledge Check
- Question 1 - Select One
Energy levels A,B,C of a certain atom corresponding to increasing values of energy i.e., EA<EB<EC. If λ1,λ2,λ3 are the wavelengths of radiations correspnding to the transitions C to B,B to A and C to A respectively, which of the following statements is correct?
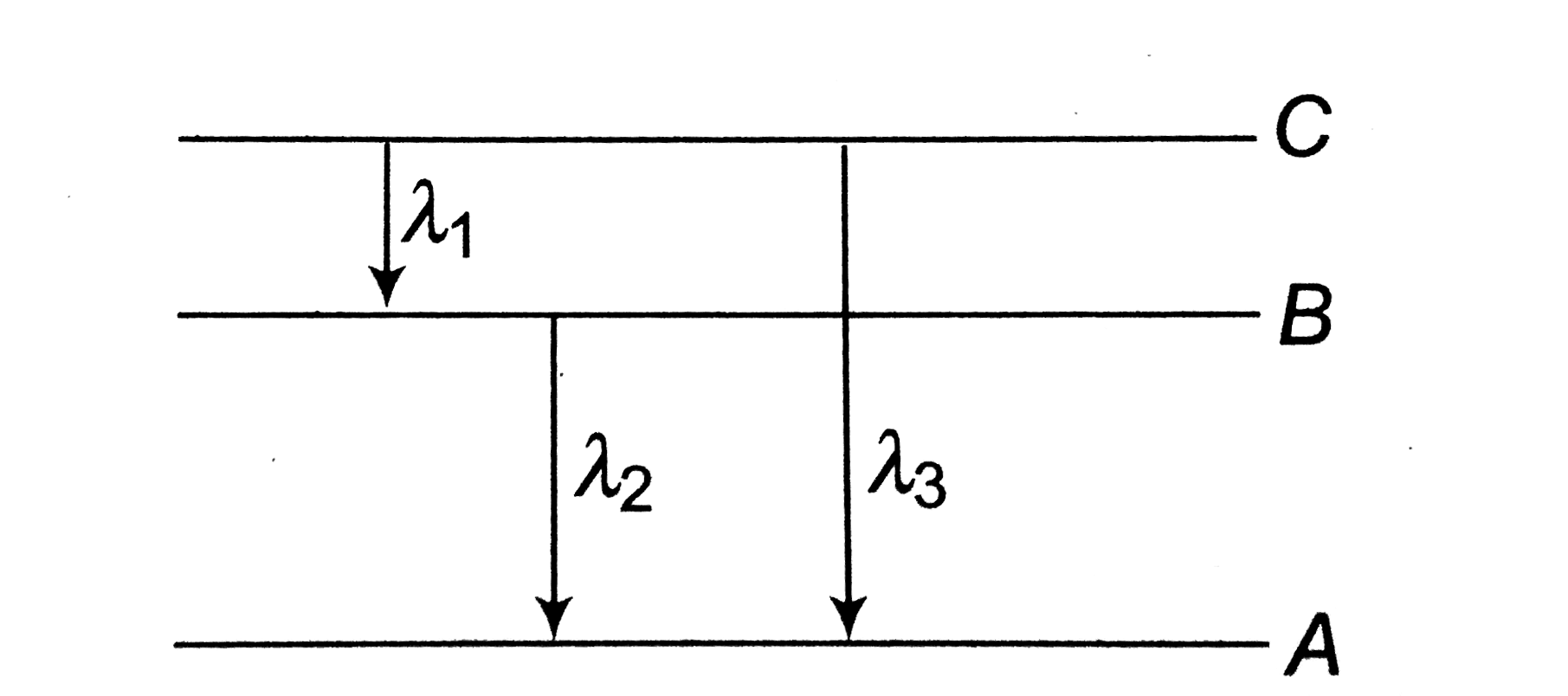 Aλ3=λ1+λ2Bλ1+λ2+λ3=0Cλ23=λ21+λ22Dλ=λ1λ2λ1+λ2
Aλ3=λ1+λ2Bλ1+λ2+λ3=0Cλ23=λ21+λ22Dλ=λ1λ2λ1+λ2
If λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View SolutionIf λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
View SolutionEnergy levels A,B,C of a certain atoms corresponding to increasing values of energy level i.e., EA<EB<EC. If λ1,λ2 and λ3 are the wavelengths of radiations corresponding to the transitions C to B,B to A and C to A respectively which of the following statement is correct?
View SolutionWavelengths of the first lines of the Lymar: series, Paschen series and Balmer series, in hydrogen spectrum are denoted by λL,λPandλB respectively. Arrange these wavelengths in increasing order.
View SolutionWavelength of light used in an optical instrument are λ1=4000Å and λ2=5000Å then ratio of their respective resolving powers (corresponding to λ1 and λ2) is
View SolutionEnergy levels A,B,C of a certain atom corresponding to increasing values of energy i.e., EA<EB<EC. If λ1,λ2,λ3 are the wavelengths of radiations correspnding to the transitions C to B,B to A and C to A respectively, which o fthe following statements is correct?
 View Solution
View SolutionA dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View Solution

