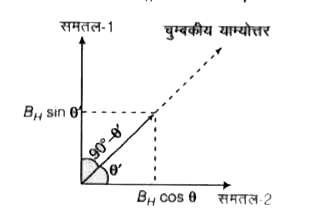
यदि एक-दूसरे से लम्बवत् दो ऊर्ध्वाधर समतलों में प्रेक्षित आभासी नमन (नति) कोण θ1 औरθ2 है, तो वास्तविक नमन कोण θ का मान किस समीकरण से प्राप्त होगा?
cot2θ=cot2θ1+cot2θ2
tan2θ=tan2θ1+tan2θ
cot2θ=cot2θ2−cot2θ2
tan2θ=tan2θ1−tan2θ2
The correct Answer is:A
माना BH व Bv पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज व ऊर्ध्वाधर घटक हैं।
अतःtanθ=BvBH।cotθ=BHBv
माना समतल (1) व (2) आपस में लम्बवत् हैं। समतल 1 व 2 क्रमशः θ व (90∘−θ) कोण चुम्बकीय याम्योत्तर के साथ बनाते हैं। पृथ्वी के चुम्बकीय क्षेत्र का ऊर्ध्वाधर घटक दोनों तलों में समान रहता है, लेकिन प्रभावी क्षैतिज घटक इन दोनों तलों में निम्न प्रकार दिए जाते हैं
B1=Bhcosθ
B2=BHsinθ
तब,tanθ1=BvB1=BvBHcosθ.
cotθ1(BHcosθ.)BV
इसी प्रकार
tanθ2=BvB2=BvBHsinθ.
=cotθ2=BHsinθ.BV
सेमी (iv ) व (v ) से
=cot2θ1+cot2θ2=B2Hcos2θ.B2v+B2Hsin2θ.B2v
=cot2θ1+cot2θ2B2HB2v(cos2θ.+sin2θ.)
[∴cos2θ+sin2θ=1]
=cot2θ1+cot2θ2=cot2θ [ सेमी ( i ) से ]
Topper's Solved these Questions
Similar Questions
n फेरों, त्रिज्या R तथा अनुप्रस्थ त्रिज्या a वाली टोरोइड में प्रवाहित धारा I है । इसे क्षैतिज मेज पर रखा जाता है , इसका चुम्बकीय आघूर्ण m होगा
View Solutionएक छड़ चुम्बक पृथ्वी के चुम्बकीय क्षेत्र में आवर्तकाल से दोलन करती है। यदि चुम्बक का द्रव्यमान 1/4 कर दे तो आवर्तकाल :
View Solutionसदिश →a और →b दो मात्रक सदिश है तथा इनके बीच का कोण α है। यदि →a+→b भी एक मात्रक सदिश है तो α का मान होगा -
View Solutionयदि दो सदिशों →a और →b के बीच का कोण θ है तो →a.→b≥0 होगा। यदि -
View Solutionयदि अक्षों को 45∘ कोण से घुमाया जाए तो वक्र x2+y2=a2 का नया समीकरण ज्ञात कीजिए ।
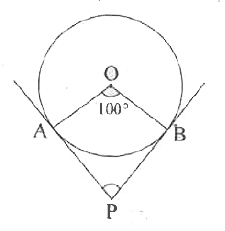
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
View Solutionएक रेखा x- अक्ष से 120∘ तथा y-अक्ष से 60∘ का कोण बनाती है, तो रेखा द्वारा z-अक्ष से बना कोण ज्ञात कीजिए।
View Solutionयदि sinθ=12 तथा θ एक अधिक कोण है , तो cotθ का मान होगा
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionदो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु की दूरी#!#एक रेखा एवं एक समतल के बीच कोण#!#उदाहरण
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View Solutionदो समतलों के मध्य कोण
View Solutionयदि कोई किरण किसी दर्पण पर 30∘ पर आपतित होती है तो परावर्तित कोण का मान होगा
View Solutionनिम्न में से किस घर्षण का मान सर्वाधिक होगा
View SolutionIn the triangle, if AB=AC and angle ABC = 72^@ , then angle BAC is: एक त्रिभुज में, यदि AB=AC तथा angle ABC = 72^@ है, तो कोण BAC का मान क्या होगा ?
View SolutionIf theta is an acute angle, and it is given that 5sin theta+12 cos theta=13 , then what is the value of tan theta ? यदि theta एक न्यून कोण है और यह दिया गया है कि 5sin theta+12 cos theta=13 है, तो tan theta का मान क्या होगा ?
View Solution
