संधारित्रों के श्रेणी संयोजन की तुल्य धारिता के लिए सम्बन्ध प्राप्त कीजिए | परिपथ चित्र बनाइये |
संधारित्रों का ऐसा संयोजन जिसमे प्रत्येक संधारित्र पर आवेश का परिमाण एक समान रहता है, उसे श्रेणी संयोजन कहते है |

चित्रानुसार C1,C2वC3 धारिता वाले संधारित्रों का श्रेणी संयोजन किया जाता है | प्रथम संधारित्र की प्लेट a1 की बैटरी के धनाग्र व तीसरे संधारित्र की प्लेट a6 को बैटरी के ऋणाग्र से जोड़ा गया है | प्लेट a1 से जितने इलेक्ट्रॉन बैटरी के धनाग्र की ओर प्रवाहित होते है | उतने ही इलेक्ट्रॉन बैटरी के ऋणाग्र से प्लेट a6 पर पहुँच जाते है | परिणामश्वरूप प्लेट a1 की अंदर की सतह पर +Q आवेश तथा प्लेट a6 की अंदर की सतह पर -Q आवेश उत्पन्न हो जाता है (इस स्थिति में प्लेट a1वa6 मिलकर एक विलगित निकाय बनाते है जिन पर कुल आवेश की मात्रा शून्य रहती है ) चूँकि प्लेट a2वa3 परस्पर जुड़े हुए है | अतः ये दोनों एक अलग विलगित निकाय होंगे, इसलिए इन दोनों पर आवेश शून्य होना चाहिए | अतः प्लेट a1 पर उपस्थित +Q आवेश के कारण उत्पन्न विधुत क्षेत्र से इलेक्ट्रॉन, प्लेट a3 से a2 की ओर गति करते है जिससे प्लेट a2 पर Q आवेश व a3 पर +Q आवेश प्रेरित हो जाता है | इसी प्रकार प्लेट a4 व प्लेट a5 पर क्रमशः -Q आवेश व +Q आवेश प्रेरित होता है | अतः श्रेणी संयोजन में प्रत्येक संधारित्र पर आवेश का परिमाण समान रहता है |
N पर विभव शून्य माना जाये तो चालक तार द्वारा बिंदु N से जुडी हुई प्लेट a6 का विभव शून्य होगा | बिंदु P और प्लेट a1 का विभव V है |
यहाँ प्लेट a2वa3 और a4वa5 परस्पर अलग-अलग है | इनके विभव के मान क्रमशः V1वV2 हो तो श्रेणीक्रम में संयोजित इन संधारित्र की प्लेटों के मध्य विभवांतर
(V−V1)=QC1 ...(1)
(V1−V2)=QC2 ...(2)
(V2−0)=QC3 ...(3)
बिंदु P और N के मध्य विभान्तर समीकरण (1), (2) व (3) को जोड़ने पर प्राप्त होगा-
V−V1+V1−V2+V2−0
=QC1+QC2+QC3=Q(1C1+1C2+1C3)
⇒V=Q(1C1+1C2+1C3)
अतः P व N के मध्य तुल्य धारिता C का मान होगा-
C=QV से
C=QQ(1C1+1C2+1C3)
=11C1+1C2+1C3
या 1C=1C1+1C2+1C3 ...(4)
इसी प्रकार जितने भी संधारित्र होंगे सभी उक्त सूत्र की तरह जुड़ जायेंगे |
इसलिए n संधारित्रों के संयोजन की तुलीधारिता
1C=1C1+1C2+1C3...1Cnहोंगी ...(5)
अतः हम कह सकते है के-
(i) संयोजन की तुल्यधारिता का व्युत्क्रम संयोजन में प्रयुक्त संधारित्र की धारिता के व्युत्क्रम के योग के बराबर होता है |
(ii) श्रेणी संयोजन में प्राप्त तुल्यधारिता का मान किसी भी संधारित्र की धारिता के मान से भी कम होता है |
Topper's Solved these Questions
- BOOK - TRIPUTI PUBLICATIONCHAPTER - स्थिर वैद्युतिकीEXERCISE - आंकिक प्रश्न5videos
स्थिर वैद्युतिकी
- BOOK - TRIPUTI PUBLICATIONCHAPTER - स्थिर वैद्युतिकीEXERCISE - लघूत्तरात्मक प्रश्न3videos
स्थिर वैद्युतिकी
- BOOK - TRIPUTI PUBLICATIONCHAPTER - वैघुत चुम्बकीय प्रेरण तथा प्रत्यावर्ती धाराEXERCISE - आंकिक प्रश्न7videos
वैघुत चुम्बकीय प्रेरण तथा प्रत्यावर्ती धारा
Similar Questions
एक समांतर पट्टिका वायु संधारित्र की धारिता 8 pF है | यदि इसकी पट्टिकाओं के बीच की दूरी आधी कर दी जाये तथा इनके बीच S परावैधुतांक का कोई पदार्थ पूर्णतः भर दे तो संधारित्र की धारिता ज्ञात कीजिए |
53:42View Solutionत्रिज्या r तथा लंबवत l के एक बेलनाकार पृष्ठ में आवेश घनत्व A तथा अनंत लम्बाई का पतला सीधा चालक तार परिबद्ध है | बेलनाकार पृष्ठ की अक्ष तार की लम्बाई के संपाती है | बेलनाकार पृष्ठ से विधुत फ्लक्स के लिए व्यंजक ज्ञात कीजिए |
56:40View Solutionकिसी परिपथ में 0.1s में धारा 5.0A से शून्य तक गिरती है । यदि औसत प्रेरित वि. वा. बल 100 वोल्ट है तो परिपथ में प्रेरक के स्वप्रेरकत्व की गणना कीजिए।
47:52View Solutionसंधारित्रों के संयोजन पर प्रश्न
34:29View Solutionसंधारित्रों के संयोजन
01:14:31View Solutionसंधारित्रों के संयोजन पर महत्वपूर्ण प्रश्न
45:22View Solutionश्रेणी अनुनादी परिपथ की विशेषताए
40:55View Solutionविभिन्न प्रकार के प्रत्यावर्ती परिपथ |प्रेरकत्व,संधारित्र तथा प्रतिरोध का श्रेणी का संयोजन
01:21:10View Solutionएसी परिपथ के प्रश्न एक एसी परिपथ की शक्ति अनुनाद
01:21:43View Solutionश्रेणी व समांतर क्रम संयोजन पर आधारित विद्युत परिपथ
45:09View Solutionपरावैद्युत का संयोजन|संधारित्रों के संयोजन पर उदाहरण |OMR
View Solutionसंधारित्रों के संयोजन पर उदाहरण |परिपथ विश्लेषण|OMR
View Solutionसंधारित्र की प्लेटो के मध्य माध्यम भरा हो तब धारिता #!#संधारित्र के संयोजन पर प्रश्न
View Solutionहाइड्रोजन परमाणु के लिए बामर श्रेणी की तीसरी रेखा की तरंग दैर्ध्य है:
View Solutionनिम्न के लिए हाइड्रोजनीकरण की ऊष्मा की तुलना कीजिए-
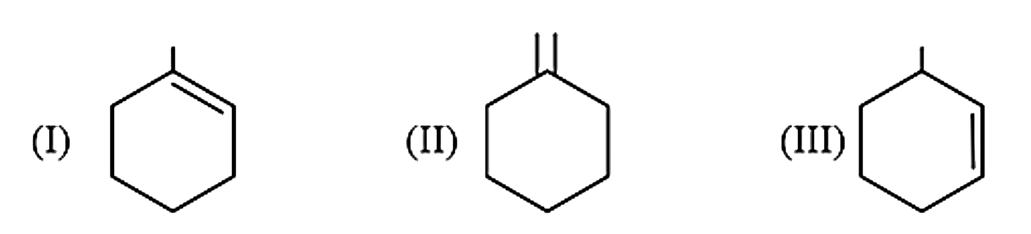 49:22View Solution
49:22View Solutionजब N2 का 80% N2O3 में परिवर्तित होता है तो N2 ,7g के साथ संयोजन के लिए आवश्यक ऑक्सीजन परमाणुओं की संख्या की गणना कीजिए।
49:35View Solution

