आइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
Step by step video & image solution for आइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T_(1)+T_(2)=4 , T_(2) + T_(3) = 9 , T_(3)+T_(4)=16 T_(4)+T_(5) के बारे में आपका क्या कहना है ? T_(n-1) +T_(n) का एक कंजेक्चर बनाइये। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - परिशिष्ट - 1 (गणित कि उपपत्तियाँ)EXERCISE - पाठ्य पुस्तक प्रश्नावली A.410videos
परिशिष्ट - 1 (गणित कि उपपत्तियाँ)
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - परिशिष्ट - 1 (गणित कि उपपत्तियाँ)EXERCISE - पाठ्य पुस्तक प्रश्नावली A1.31videos
परिशिष्ट - 1 (गणित कि उपपत्तियाँ)
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास के लिए प्रश्न4videos
निर्देशांक ज्यामिति
- BOOK - MBD HINDI-HARYANA BOARDCHAPTER - परिशिष्ट -2EXERCISE - प्रश्न40videos
परिशिष्ट -2
Similar Questions
निम्नलिखित कथनो को असत्य सिद्ध करने के लिए प्रत्युदाहरण ज्ञात कीजिये।
यदि दो त्रिभुजों के संगत कोण बराबर हो , तो त्रिभुज सर्वागसम होते है05:52View Solutionकोई भी तीन क्रमागत सम संख्याएँ लीजिये और उनका गुणनफल ज्ञात कीजिये : उदाहरण के लिए , 2×4×6=48,4×6×8=192 , आदि। इन गुणनफलो के तीन कंजेक्चर बनाइये।
03:06View Solutionबिंदुओ (5,0)(0,5)(2,5)(5,2)(−3,5)(−3,5)(−3,−5)(5,−3) और (6,1)को कार्तीय तल में चिन्हित कीजिए।
03:15View Solutionनिम्नलिखित संख्याओं में अपरिमेय संख्या कौन-सी है ?
01:39View SolutionIf T0,T1,T2,,Tn represent the terms in the expansion of (x+a)n, then find the value of (T0−T2+T4−)2+(T1−T3+T5−)2n∈N.
04:22View SolutionIn an A.P.if S_(1)=T_(1)+T_(2)+T3+...+T_(n) (n odd S_(2)=T_(1)+T_(3)+T_(5)+...+T_(n) then (S_(1))/(S_(2))=
05:45View SolutionIf tn=14(n+2)(n+3) for n=1,2,3,.... then 1t1+1t2+1t3+....+1t2003=
06:54View SolutionIf {tn} is n A.p. such that t4t1=23, find t8t9.
04:57View Solutionयदि एक वृत्त किसी समकोणीय अतिपरवलय से चार बिन्दुओं t1,t2,t3 तथा t4 में मिलता है, तो सिद्ध कीजिए कि t1,t2,t3,t4=1.
02:26View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View SolutionLet Tk=sinkx+coskxFor all x if T1T5+T3T5=T1T7+T3Tnthen n=
05:40View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
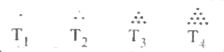
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।01:51View SolutionFind the terms (s) indicated in each case:
(i) tn=tn−1+3(n>1),t1=1,t4
(ii) Tn=Tn−1Tn−2,(n>2),T1=1,T2=2,T606:44View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to04:31View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
05:52View Solution