यदि एक वृत्त किसी समकोणीय अतिपरवलय से चार बिन्दुओं t1,t2,t3 तथा t4 में मिलता है, तो सिद्ध कीजिए कि t1,t2,t3,t4=1.
माना वृत्त x2+y2+2gx+2fy+c1=0 तथा अतिपरवलय xy=c2 है।
अतिपरवलय पर बिन्दु (ct,ct) है |
यह बिन्दु वृत्त पर स्थित है, तब
c2t2+c2t2+2gct+2f(c)t+c1=0
या c2t4+c2+2gct3+2fct+c1t2=0
या c2t4+2gct3+c1t2+2fct+c2=0
या t4+2gct3+c1c2t2+2fct+1=0
माना t के चार मूल t1,t2,t3,t4 हैं |
तब समीकरण सिद्धान्त से,
t1.t2.t3.t4=अचर परt4 का गुणांक=11=1.
Topper's Solved these Questions
- शंकु परिच्छेद BOOK - MANOHAR RAYCHAPTER - शंकु परिच्छेद EXERCISE - प्रश्नावली 11(A)
16 Videos
- शंकु परिच्छेद BOOK - MANOHAR RAYCHAPTER - शंकु परिच्छेद EXERCISE - प्रश्नावली 11(B)
16 Videos
- रैखिक असमिकाएँBOOK - MANOHAR RAYCHAPTER - रैखिक असमिकाएँEXERCISE - प्रश्नावली 6(D)
19 Videos
- समुच्चयBOOK - MANOHAR RAYCHAPTER - समुच्चयEXERCISE - प्रश्नावली 1(G)
23 Videos
Similar Questions
उस वृत्त का समीकरण ज्ञात कीजिए, जिसका :
केन्द्र (2, 3) तथा त्रिज्या 5 है।
View Solutionउन व्रतों के केन्द्र और त्रिज्याएँ ज्ञात कीजिय, जिनके समीकरण निम्नलिखित हैं-
x2+y2+2gx+2fy+c=0
View Solutionअसमिका 4x+3<6x+7 का हल होगा -
View SolutionALLAHABAD शब्द में आये हुए (A ) स्वरों का (B ) अक्षरों का समुच्चय लिखो
View SolutionThe base of a triangle is divided into three equal parts. If t1,t2,t3 are the tangents of the angles subtended by these parts at the opposite vertex, prove that (1t1+1t2)(1t2+1t3)=4(1+1t22).
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View SolutionIf {tn} is n A.p. such that t4t1=23, find t8t9.
View Solution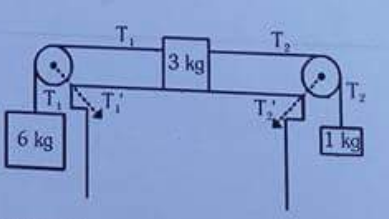
Calculate a, T1,T2,T1'&T2'.
View SolutionIf the sequence t1,t2,t3,… are in A.P. then the sequence t6,t12,t18,… is
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View SolutionFind the terms (s) indicated in each case:
(i) tn=tn−1+3(n>1),t1=1,t4
(ii) Tn=Tn−1Tn−2,(n>2),T1=1,T2=2,T6
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View Solution
