आकृति में , ΔABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD⊥BC , OE⊥AC और OF⊥AB है । दर्शाइए कि
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2 .
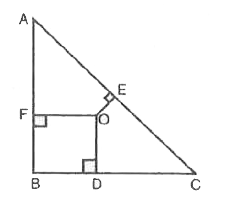
Step by step video & image solution for आकृति में , DeltaABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD bot BC , OE bot AC और OF bot AB है । दर्शाइए कि (i) OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+CE^2 (ii) AF^2+BD^2+CE^2=AE^2+CD^2+BF^2 . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - अभ्यास के लिए प्रश्न
47 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्न
11 Videos
- त्रिभुजBOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिभुजEXERCISE - प्रश्नावली 6.4
9 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - MBD HINDI-HARYANA BOARDCHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - बहुविकल्पी प्रश्न
7 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - MBD HINDI-HARYANA BOARDCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - लघु उत्तरात्मक प्रश्न
21 Videos
Similar Questions
भुजाओ की समान संख्या वाले बहुभुज समरूप होते है |
View Solutionकिसी त्रिभुज में , एक भुजा के समांतर अन्य दो भुजाओं को भिन्न - भिन्न बिंदुओं पर प्रतिच्छेद करने के लिए , एक रेखा खींची जाए , तो यह अन्य दो भुजाओं को एक ही अनुपात में विभाजित करती है । सिद्ध कीजिए ।
View Solutionमान लीजिए ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64cm2 और 121cm2 हैं । यदि EF = 15.4 cm हो , तो BC ज्ञात कीजिए ।
View Solutionपहाड़ी के शिखर से उसके पाद के 40 किमी दूरी का अवनमन कोण 45∘ है । पहाड़ी की ऊँचाई होगी :
( A ) 30 किमी ( B ) 35 किमी
( C ) 40 किमी ( D ) 45 किमी ।
View Solutionनिम्न रैखिक समीकरण के युग्म को हल कीजिए ।
2x+3y=13
5x−4y=−2
View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View Solutionआकृति 6 . 54 में ΔABC के अभ्यन्तर में स्थित कोई बिंदु O है तथा OD⊥BC,OE⊥AC और OF⊥AB है दर्शाइए कि
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
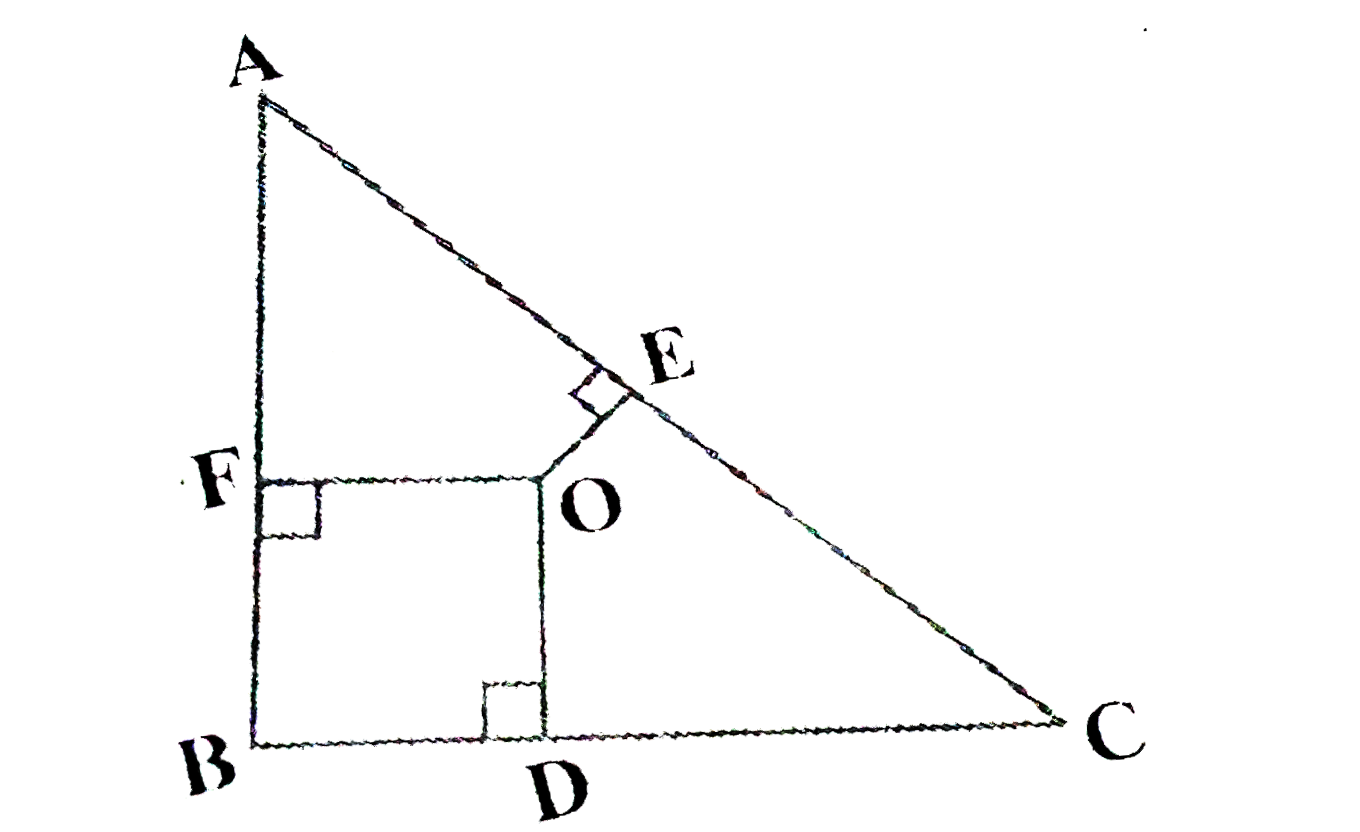
View SolutionO is a point in the interior of ΔABC,OD⊥BC,OE⊥ACandOF⊥AB, as shown in the figure,
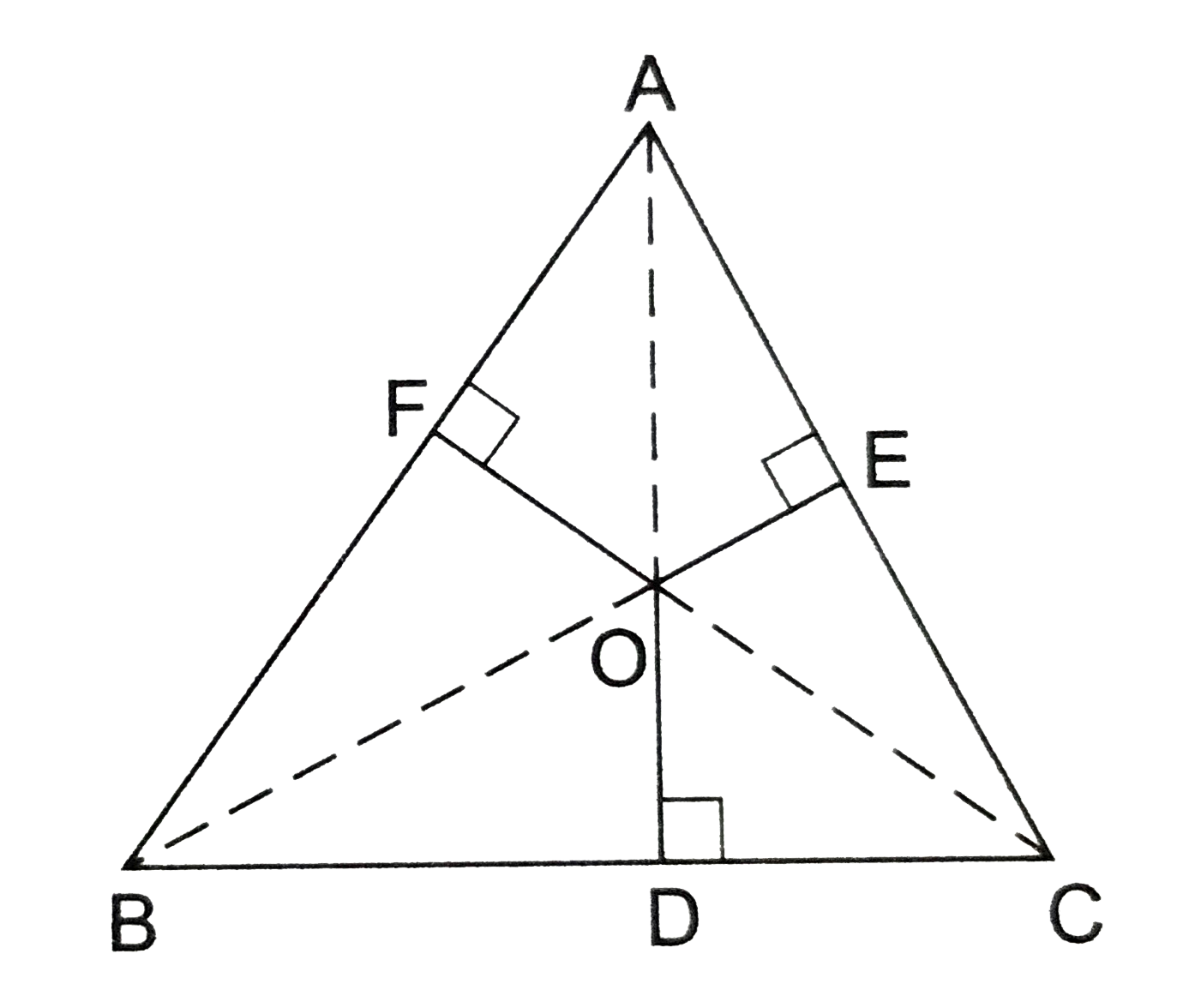
Prove that :
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD2
View Solution△ABC के एक अन्तः बिंदु O से, भुजा BC,CA तथा AB पर लम्ब क्रमशः OD,OE व OF खींचे गये है | सिद्ध कीजिए कि
(i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमशः लंब OD,OE और OF डाले गए है । सिद्ध कीजिए कि AF2+BD2+CE2=AE2+CD2+BF2.
View SolutionIn fig . O is a point in the interior of a triangle ABC , OD ⊥BC,OE⊥ACandOF⊥AB . Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2+AE2+CD2+BF2 .
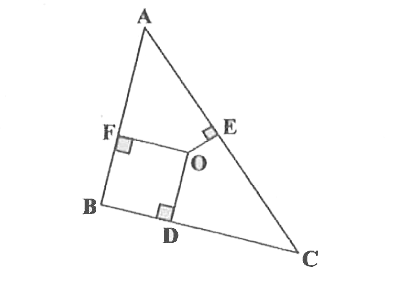
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన AE2+BF2+CD2=AF2+BD2+CE2 అని చూపండి.
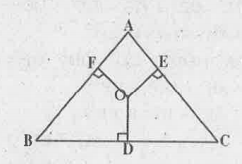
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
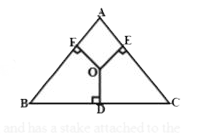
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
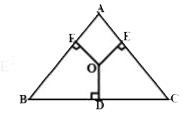
View SolutionIn the figure given below, O is point in the interior of a triangle ABC, OD⊥BC, OE⊥AC and OF⊥AB. Show that
(i) OA2+OB2+OC2+OD2−OE2−OF2=AR2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
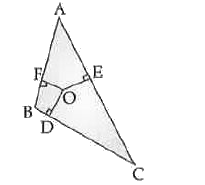
View Solution
