O is a point in the interior of , as shown in the figure,
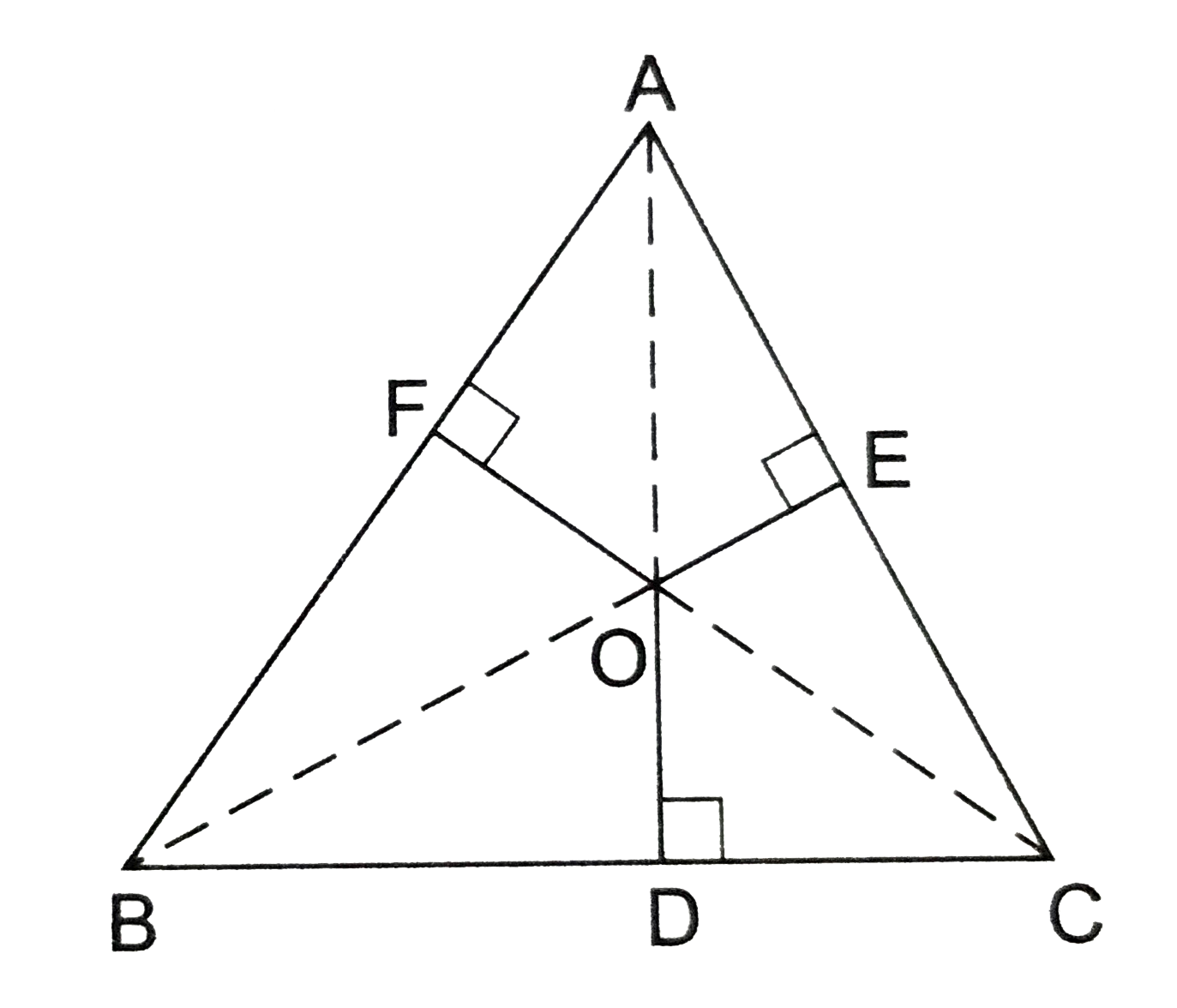
Prove that :
(ii)
Using Pythagora's theorem for each of the right triangles namely , we get
Adding, (i), (ii)n and (iii),we get
Hence,
(ii) Using Pythagora's theorem for each of the right triangles, nemely , we get
Similarly, we have
Adding the corresponding sides of (iv), (v) and (vi), we get
Hence,
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
From a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionIn the figure given below O is a point in the interior of a triangle ABC , OD ⊥ BC ,OE ⊥ AC and OF⊥AB . Show that

AF2+BD2+CE2=AE2+CD2+BF2
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn the given figure if AD ⊥ BC prove that AB2+CD2=BD2+AC2

View SolutionABCD is a rhombus. Prove that AB2+BC2+CD2+DA2=AC2+BD2
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
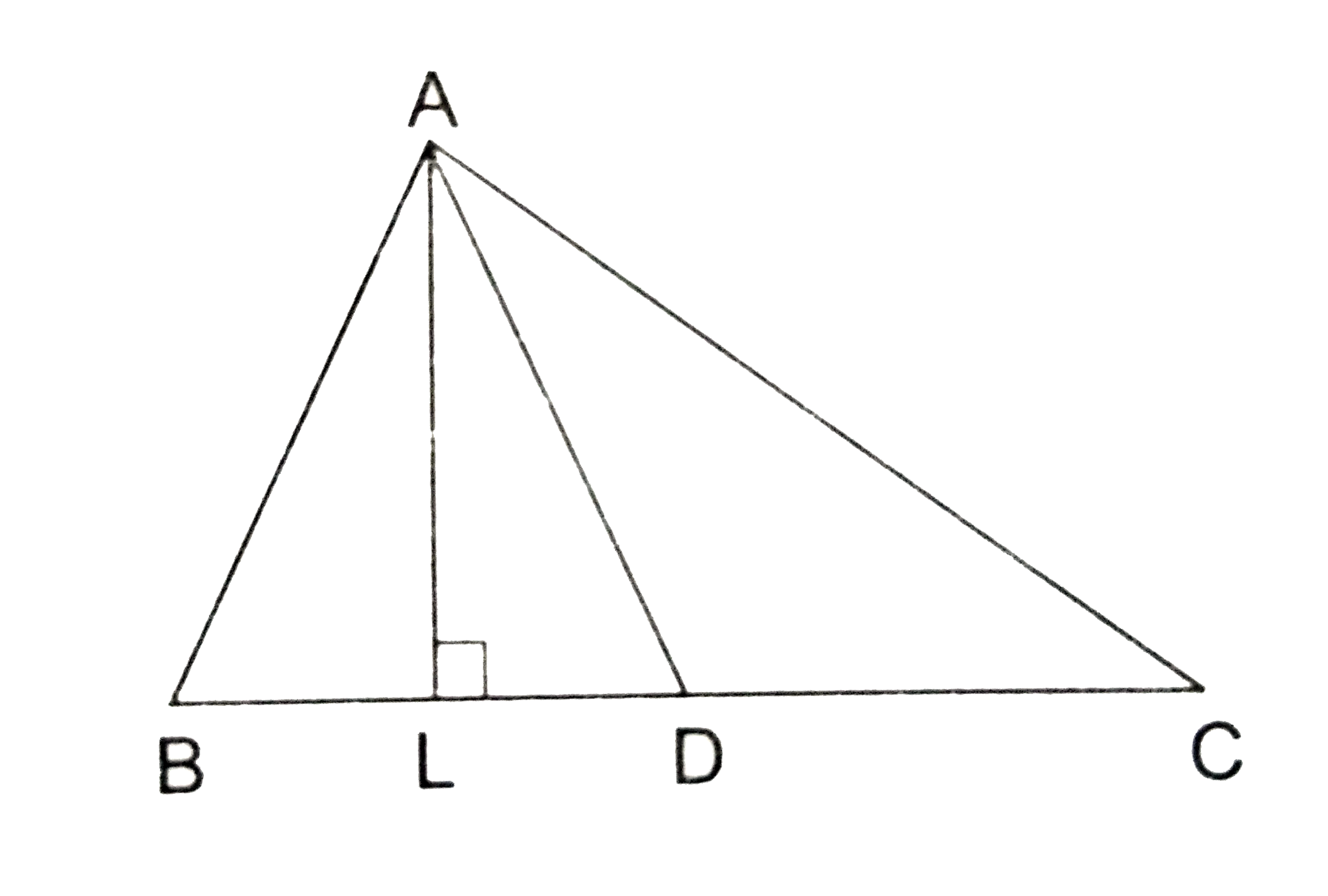
View SolutionIn aΔABC,AD is a median and AL⊥BC.
Prove that
(a) AC2=AD2+BC⋅DL+(BC2)2
(b) AB2=AD2−BC⋅DL+(BC2)2
(c) AC2+AB2=2AD2=2AD2+12BC2
View Solution
