Assertion : प्वाइन्टिंग वेक्टर (Poynting vector ) →S का औसत परिमाण, वैद्युतचुम्बकीय तरंग की तीव्रता है।
Reason: प्वाइन्टिंग वेक्टर →S=→E×→B2μ0
Assertion और Reason दोनों सत्य हैं और Reason, Assertion की सही व्याख्या है।
Assertion और Reason दोनों सत्य हैं परन्तु Reason, Assertion की सही व्याख्या नहीं है।
Assertion सत्य है परन्तु Reason असत्य है।
Assertion और Reason दोनों असत्य हैं।
The correct Answer is:A
प्वाइन्टिंग वेक्टर →S=→E×→Bμ0
क्योंकि समतल विद्युतचुंबकीय तरंग के लिए →E⊥→B,
इसलिए S=EBμ0=E0B0sin2(kx−ωt)
और Sऔसत=1T∫T0Sdt=1T∫T0E0B0μ0sin2(kx−ωt)dt
=E0B02μ0 = विद्युतचुंबकीय तरंग की तीव्रता( क्योंकि ∫T0sin2(kx−ωt)dt=T/2)
Topper's Solved these Questions
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रतियोगिता साम्रगी पूर्णांक उत्तर वाले प्रश्न4videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रतियोगिता साम्रगी सत्य या असत्य15videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रतियोगिता साम्रगी कॉलम मिलाना4videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युत विभवEXERCISE - विषय आधारित अभ्यास (प्रतिरूपी अभ्यास)12videos
वैद्युत विभव
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय प्रेरण EXERCISE - NCERT पाठ्यपुस्तक अभ्यास: उत्तरों सहित (अतिरिक्त अभ्यास)3videos
वैद्युतचुम्बकीय प्रेरण
Similar Questions
E = 58.3 N/C वाली एक वैद्युतचुम्बकीय तरंग के लिए ऊर्जा प्रवाह प्रति यूनिट क्षेत्रफल (SI यूनिटों में) _____ है
03:43View Solutionमैक्सवेल के समीकरण केवल उन्हीं क्षेत्रों पर लागू होते हैं, जो समय के साथ स्थिर रहते हैं।
02:02View Solutionकॉलम-I में दी गई भौतिक राशियों को उनके लिए कॉलम-II में दिए गए व्यंजकों से मिलाएँ:
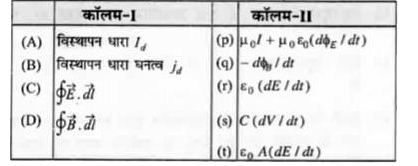 02:11View Solution
02:11View Solutionपृथ्वी पर किसी जगह आसमानी बिजली गिरती है और 1.00×108V के विभवान्तर पर बादल से पृथ्वी को -20.0 C का आवेश देती है।
(a) क्या बादल उच्च विभव पर है या पृथ्वी?
(b) पृथ्वी को कितनी ऊर्जा दी जाती है?
(c) यदि इस ऊर्जा को एक 100 W के बिजली के बल्ब को जलाने के लिए प्रयोग किया जा सकता, तो यह कितने दिन चलेगी?02:19View Solution12cm भुजा वाला एक वर्गाकार लूप, जिसकी भुजाएँ X और Y अक्षों के समान्तर हैं, 8 cm/s के वेग से धनात्मक X-दिशा में ऐसे स्थान में चलाया जाता है जिसमें धनात्मक Z-दिशा में चुम्बकीय क्षेत्र है। क्षेत्र न तो आकाश में एकसमान है और न ही समय के साथ स्थिर। इसकी प्रवणता ऋणात्मक X-दिशा में 10−3T/cm है (अर्थात् ज्यों ज्यों ऋणात्मक X-दिशा में जाएँ, यह 10−3T/cm बढ़ता है) और यह समय के साथ 10−3T/s की दर से घट रहा है। लूप में प्रेरित धारा की दिशा और परिमाण निकालें यदि इसका प्रतिरोध 4.50mΩ हो।
01:52View SolutionAssertion: If ∣∣→A+→B∣∣=∣∣→A−→B∣∣, then angle between →A and →B is 90∘
Reason: →A+→B=→B+→A04:42View SolutionAssertion: If vec(A).vec(B)= vec(B).vec(C ) , then vec(A) may not always be equal to vec(C ) . Reason: The dot product of two vectors involves consine of the angle between the two vectors.
01:27View SolutionAssertion: Vector product of two vectors is an axial vector.
Reason: If →v= instantaneous Velocity, →r= radius vector and →ω= angular velocity, then →ω=→v×→r.03:01View SolutionAssertion: →τ=→r×→F and →τ≠→F×→r
Reason: Cross product of vectors is commutative.01:36View SolutionAssertion: If dot product and cross product of vec(A) and vec(B) are zero, it implies that one of the vector vec(A) and vec(B) must be a null vector. Reason: Null vector is a vector with zero magnitude.
View SolutionPoynting vectors vec(S) is defined as vec(S)=(1)/(mu_(0))vec(E)xx vec(B) . The average value of 'vec(S)' over a single period 'T' is given by
View SolutionPoynting vector vec P for an EM wave is
04:32View SolutionIf →a and →b are unit vectors, then the vectors (→a+→b)×(→a×(→b) is parallel to the vector.
View SolutionStatements: - Pointing vector vecS The average magnitude of is the intensity of the electromagnetic wave. Reason: - Pointing vector vecS=(vecExxvecB)/(2mu_0) Is given by
44:12View Solution(A) : Electromagnetic waves are tranverse in nature. (R) : The Poynting,s vector which gives the power density is given by vecP=vecExxvecB
05:53View Solution
