नगण्य द्रव्यमान वाली एक रस्सी, 20kg द्रव्यमान एवं 20cm त्रिज्या के गतिपालक पहिये के रिम पर लपेटी हुई है। रस्सी पर 25N का एकसमान कर्षण बल लगाया जाता है जैसा कि चित्र में दर्शाया गया है। गतिपालक पहिया एक क्षैतिज धुरी पर लगाया गया है जिसके बियरिंगों में कोई घर्षण नहीं है।
(a) पहिये के कोणीय त्वरण की गणना कीजिए।
(b) 2m रस्सी खुलने तक कर्षण बल द्वारा किया गया कार्य ज्ञात कीजिए।
(c) इस क्षण पर पहिये की गतिज ऊर्जा ज्ञात कीजिए। यह मानिए कि पहिया शून्य से गति प्रारंभ करता है।
(d) भाग (b) एवं (c) के उत्तरों की तुलना कीजिए।

(a) ∴ बल आघूर्ण τ=FR=25×0.20=5 न्यूटन मीटर
पहिये का अपनी अक्ष के परित जड़त्व आघूर्ण
I=MR22
=20×(0.20)22
=0.40 किग्रा. × मी2
∴τ=Iα
∴ कोणीय त्वरण α=τI
=5.00.4=12.5 रेडियन/सेकण्डर2
(b ) मीटर रस्सी खोलने में किया गया कार्य
=25×2=50 जूल
(c ) पहिये का कोणीय विस्थापन
θ=खोली गई रस्सी की लम्बाईपहिये की त्रिज्या
=20.20=10 रेडियन
∴ पहिया विरामावस्था से गति प्रारंभ करता है।
यदि ω अंतिम कोणीय वेग है तब
Ω2=ω2_∘+2αθ
=0+2×12.5×10
=250 (रेडियन /सेकण्ड)2
∴ गतिज ऊर्जा में वृद्धि =12Iω2
=12×0.4×250
=50 जूल
(d ) यहाँ भाग (b) तथा (c) दोनों के उत्तर समान है अर्थात् पहिये द्वारा प्राप्त गतिज ऊर्जा = बल द्वारा किया गया कार्य इसका कारण कि घर्षण के कारण ऊर्जा का क्षय नहीं हुआ है
Topper's Solved these Questions
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - TEST YOUR KNOWLEDGE
20 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - MCQs
11 Videos
- उष्मागतिकीBOOK - SCIENCE PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
28 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकित प्रश्न ) टक्करों पर आधारित प्रश्न
8 Videos
Similar Questions
घूर्णन गति से क्या तात्पर्य है?
View Solutionयदि HCI अणु में H' की द्रव्यमान-केन्द्र से दूरी x हो तो CI35 की दूरी होगी
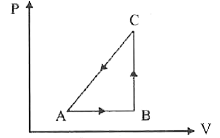
View Solutionएक निकाय का P-V आरेख जो कि ऊष्मागतिकी परिवर्तन प्रदर्शित करता है। चित्र में दर्शाया गया है। निकाय पर किया गया कार्य A→B→C 50J है ,आंतरिक ऊर्जा में परिवर्तन ज्ञात कीजिये,दी गई ऊष्मा 84 J है।
View Solutionदो किलोग्राम द्रव्यमान का एक पिण्ड किसी अन्य स्थिर पिण्ड से पूर्णतः अप्रत्यास्थ टक्कर करता है। यदि टक्कर के बाद दोनों पिण्ड उसी दिशा में पहले पिण्ड की एक चौथाई चाल से गतिमान हो तो दुसरे पिण्ड का द्रव्यमान ज्ञात करिये।
View Solutionघर्षण बल के द्वारा किया गया कार्य
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionरस्सी व द्रव्यमान पर मत्वपूर्ण प्रश्न
View Solutionएक काय केंद्रित घनीय जालक का निर्माण B के खोखले गोलों से किया गया है। ठोस A के गोले, B के खोखले गोलों में उपस्थित है। A की त्रिज्या, B की त्रिज्या की आधी है। एकक कोष्ठिका में, A द्वारा अनअधिधारित B के गोलों के कुल आयतन और एकक कोष्ठिका के आयतन का अनुपात क्या है?
View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View Solutionजब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionपरमाणु का नाभिक गोलाकार होता है। नाभिक की त्रिज्या और द्रव्यमान संख्या A के बीच संबंध 1.25×10−13×A13cm द्वारा दिया गया है। यदि परमाणु की त्रिज्या एक A है और द्रव्यमान संख्या 64 है, तब नाभिक द्वारा ग्रहण किये गए परमाण्विक आयतन का प्रभाज (x)×10−13 है। x की गणना कीजिए।
View Solutionजलीय विलयन में FeCl3,K4[Fe(CN)6] के साथ अभिक्रिया करने पर नीला रंग देता है। ये एक अर्धपारगम्य झिल्ली AB द्वारा अलग किए जाते हैं जैसा कि चित्र में दिखाया गया है। परासरण के कारण

View Solutionएक साइक्लोहेक्सेनोन, अम्ल उत्प्रेरक मात्रा की उपस्थिति में डाइमेथिलएमीन के साथ अभिक्रिया पर एक यौगिक का निर्माण करता है, यदि अभिक्रिया के दौरान जल का लगातार निष्कासन किया जाता है, तब निर्मित यौगिक को सामान्यतः जाना जाता है
View Solution
