किसी लेन्स से प्रकाश के अपवर्तन के लिए न्यूनतन का सूत्र x1x2=f1f2 स्थापित कीजिए, जहाँ लेन्स के प्रथम फोकस से वस्तु की दुरी प्रथम एवं द्वितीय फोकस दूरियाँ है| इसकी सहायता से सिद्ध कीजिए की लेन्स की कितनी फोकस दुरी पर वस्तु का प्रतिबिम्ब अनंत पर बनेगा |
प्रकाश के अपवर्तन के लिए न्यूनतन के सूत्र की उपपत्ति- माना पतले उत्तल लेन्स L की मुख्य अक्ष पर एक वस्तु AB अक्ष के लम्बवत सहित है (चित्र) | बिंदु F1 तथा बिंदु F2 लेन्स के क्रमश: प्रथम व् द्वितीय फोकस है | बिंदु B से लेन्स के मुख्य अक्ष के समांतर किरण BF लेन्स से अपवर्तन के पश्चात लेन्स के द्वितीय फोकस F2 से होकर जाती है | दूसरी किरण BC प्रथम फोकस F1 से गुजरकर अपवर्तन के पश्चात् मुख्य अक्ष के अमंतर हो जाती है | ये दोनों अपवर्तित किरणे बिन्दु D पर मिलती है तथा DE मुख्य अक्ष पर अभिलम्ब है, अत: लेन्स द्वारा वस्तु AB का प्रतिबिम्ब DE बनता है |
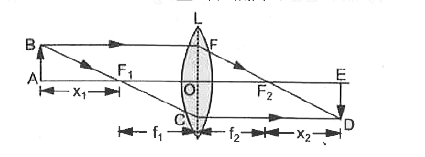
माना वस्तु AB तथा प्रतिबिम्ब DE की क्रमश: F1 तथा F2 से दूरियाँ x1 तथा x2 है, जबकि लेन्स की बायु ओर के माध्यम में फोकस दुरी f1 तथा दाई ओर के माध्यम में फोकस दुरी f2 है |
समरूप ΔABF1 तथा ΔOCF1 में,
ABOC=AF1OF1 . . (1)
तथा समरूप ΔOFF2 तथा ΔDEF2 में,
OFDE=OF2F2E
परन्तु OF=AB तथा DE=OC,
अत: ABOC=OF2F2E . . (2)
अत: समीकरण (1) तथा समीकरण (2) से,
AF1OF1=OF2F2E
अथवा AF1×F2E=OF1×OF2 . . (3)
परन्तु AF1=−x1 व् F2E=x2
तथा OF1=−f1 व् OF2=f2
ये मान समीकरण (3) में रखने पर,
(−x1)x2=(−f1)f2
अत: x1x2=f1f2
यही लेन्स द्वारा अपवर्तन के लिए न्यूटन का व्यापक सूत्र है|
सूत्र 1f=1v−1u से,
1v=1f+1u=1f+1−f=0
अत: v=∞
Topper's Solved these Questions
Similar Questions
कांच-जल के मध्य पृष्ठ पर क्रांतिक कोण ज्ञात कीजिए यदि वायु के सापेक्ष कांच एवं जल के अवपरतणंक क्रमश: 3/2 एवं 4/3 है !
View Solutionदो समान्तर धारावाही तारों के मध्य में चुम्बकीय क्षेत्र का मान B है जबकि तारों में क्रमशः i तथा 2i धारायें बह रही है। यदि धारा i वाले टनों में धारा का मान शून्य कर दिया जाये तब चुम्बकीय क्षेत्र का मान क्या होगा?
View Solutionएक बिंदु वस्तु एक काँच जिसका अपवर्तनांक (μs=32) है, से बने 20 सेमी फोकस दूरी वाले उत्तल लेन्स से 30 सेमी की दूरी पर रखी है। वस्तु का अन्तिम प्रतिबिमब अनन्त पर बनेगा यदि
View Solutionलेंस की फोकस दूरी की निर्भरता|लेंस सूत्र तथा संयुग्मी फोकस
View Solutionएक लेंस 10 सेमी दूरी पर रखी वस्तु का तीन गुना बड़ा आभासी प्रतिबिम्ब बनाता है। लेंस की प्रकृति, फोकस दूरी तथा प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
View SolutionRevision|हीरोन के सूत्र की सहायता से त्रिभुज का क्षेत्रफल निकलना सीखे#!#परीक्षा की दृष्टि से महत्वपूर्ण प्रश्न#!#Quiz की सहायता से Revision
View Solutionचतुर्भुज का क्षेत्रफल निकलना सीखे|हीरोन के सूत्र की सहायता से#!#महत्वपूर्ण प्रश्न
View Solutionफोकस दुरी वक्रता त्रिज्या में सम्बन्ध#!#दर्पण सूत्र व उस पर आधारित प्रशन
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionउचित संबंध जोडिए-
'क''ख'वस्तु की स्थितिप्रतिबिम्ब की स्थिति1. F पर(a) F और 2F के बीच2. F और 2F के बीच(b) वस्तु की ओर ही3. 2F से परे(c) अनंत पर4. F और प्रकाश केन्द्र के बीच(d) 2F से परे।
View Solutionवस्तु की गुरत्वाकर्षण के अधीन गति #!#वस्तु की गुरत्वाकर्षण के अधीन गति पर प्रश्न
View Solutionवस्तु की गुरत्वाकर्षण के पर प्रश्न
View Solution.0.12 मी फोकस, दूरी के उत्तल लेन्स से वस्तु का तीन गुना वास्तविक प्रतिबिम्ब पर्दे पर प्राप्त करने के लिए वस्तु को लेन्स से दूर रखना
View Solutionकिसी निश्चित राशि पर 4% प्रतिवर्ष, ब्याज की दर से दो वर्षों के चक्रवृद्धि ब्याज एवं साधारण ब्याज का अन्तर ₹ 20 है, तो मूलधन की राशि कितनी थी?
View Solutionकिसी धातु की प्रथम और द्वितीय आयनन एन्थैल्पीयाँ क्रमश: 496 और 4560kJmol−1 है। धातु हाइड्रॉक्साइड के 1 मोल के साथ पूरी तरह से अभिक्रिया करने के लिए क्रमशः HCI और H2SO4 के कितने मोलों की आवश्यकता होगी?
View Solutionपतले लेंस के लिये अपवर्तन सुत्र#!#लेंस की फोकस दूरी की निर्भरता
View Solution