किसी पतले लेन्स के लिए अपवर्तन का सूत्र स्थापित कीजिए | इसके आधार पर सिद्ध कीजिए की अवतल लेन्स की फोकस दुरी ऋणात्मक होती है |
गोलीय पृष्ठ पर प्रकाश के अपवर्तन का सूत्र निम्नलिखित है -
nv−1u=n−1R
पतले लेन्स के लिए अपवर्तन का सूत्र-माना एक पतला उत्तल लेन्स L वायु में रखा है | लेन्स के पदार्थ का वायु के सापेक्ष अपवर्तनांक n2 है लेन्स के दोनों ओर माध्यम समान है जिसका अपवर्तनांक n1 है | माना लेन्स का प्रकाशिक केंद्र C है तथा इसके पहले व् दुसरे पृष्ठों की वक्रता त्रिज्याएँ क्रनाश: R1 व् R2 है | माना लेन्स की मोटाई t है | माना लेन्स के मुख्य अक्ष पर एक बिंदु-वस्तु O, प्रथम पृष्ठ के ध्रुव P1 से u दुरी पर रखी है |
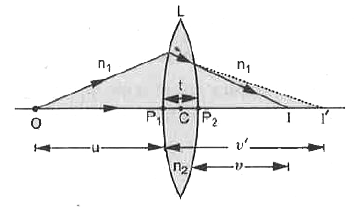
माना किरणे माध्यम n1 से माध्यम n2 की ओर जा रही है, अत: प्रथम गोलीय पृष्ठ पर अपवर्तन के सूत्र से,
n2v.−n1u=n2−n1R1 . . (1)
यह प्रतिबिम्ब I. द्रितीय पृष्ठ के लिए आभासी वस्तु का कार्य करता है | प्रतिबिम्ब I. की द्रितीय पृष्ठ के ध्रुव P2 से दुरी (v.−t) होगी " द्रितीय पृष्ठ द्वारा I. का अंतिम प्रतिबिम्ब I इस पृष्ठ के ध्रुव P2 से v दुरी पर बनता है |
अत: n1v−n2(v.−t)=(n1−n2)R2 . . (2)
पतले लेन्स के लिए t का मान v के सापेक्ष उपेक्षीय है | अत: समीकरण (2) से ,
n1v−n2v.=n1−n2R2=−(n2−n1)R2 . . (3)
समीकरण (1) व् समीकरण (3) को जोड़ने पर,
n1v−n1u=(n2−n1)(1R1−1R2)
अथवा 1v−1u=(n2n1−1)(1R1−1R2)
अथवा 1v−1u=(1n2−1)(1R1−1R2)
हम जानते है की जब कोई वस्तु अनंत पर होती है तो प्रतिबिम्ब लेन्स के द्वितीय फोकस पर बनता है, अर्थात जब u=∞ है तो v=f.
अत: 1f−1∞=(1n2−1)(1R1−1R2)
अथवा 1f=(1n2−1)(1R1−1R2) . . (4)
यदि प्रथम माध्यम वायु तथा लेन्स के पदार्थ का अपवर्तनांक n हो तो यह मान समीकरण (4) में रखने पर
1f=(n−1)(1R1−1R2)
यही पतले लेन्स के लिए अपवर्तन का सूत्र है |
अवतल लेन्स के लिए R1 ऋणात्मक तथा R2 धनात्मक होता है तथा
अत: 1f=(n−1)(1−R1−1R2)=−(n−1)(1R1+1R2)
अत: अवतल लेन्स की फोकस दुरी ऋणात्मक होती है |
दिया है, ang=1.5,anw=4/3,fa=10 सेमी
वायु में फोकस दुरी, 1fa=(ang−1)(1R1−1R2)
जल में फोकस दुरी, 1fw=(anganw−1)(1R1−1R2)
∴fwfa=(ang−1)(anganw−1)
या fw10 सेमी =(1.5−1)(1.54/3−1)=0.50.5×4
या fw=40 सेमी |
Topper's Solved these Questions
Similar Questions
कांच-जल के मध्य पृष्ठ पर क्रांतिक कोण ज्ञात कीजिए यदि वायु के सापेक्ष कांच एवं जल के अवपरतणंक क्रमश: 3/2 एवं 4/3 है !
View Solutionदो समान्तर धारावाही तारों के मध्य में चुम्बकीय क्षेत्र का मान B है जबकि तारों में क्रमशः i तथा 2i धारायें बह रही है। यदि धारा i वाले टनों में धारा का मान शून्य कर दिया जाये तब चुम्बकीय क्षेत्र का मान क्या होगा?
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionकाव्यांश के आधार पर परशुराम के स्वभाव की दो विशेषताओं पर सोदाहरण टिप्पणी कीजिए।
View Solutionअट नहीं रही है' कविता के आधार पर बसंत ऋतु की शोभा का वर्णन कीजिए।
View Solution'अट नहीं रही है' कविता के आधार पर वसंत ऋतु की शोभा का वर्णन कीजिए।
View Solutionजीवन मूल्यों के आधार पर इफ्फन और टोपी शुक्ला के संबंधों की समीक्षा कीजिए।
View Solutionमानवीय मूल्या के आधार पर इफ्फन आर टापाशुक्ला का दोस्ती की समीक्षा कीजिए।
View Solutionमीरा के पदों के आधार पर स्पष्ट कीजिए कि वह भक्त की विपत्ति दूर करने के लिए किन प्रसंगों की याद कृष्ण को दिखाती है और उन्हें पाने के लिए क्या-क्या कार्य करने को तत्पर है?
View Solutionअथवा 'कारतूस' पाठ के आधार पर वज़ीर अली की चारित्रिक विशेषताओं का उदाहरण सहित वर्णन कीजिए।
View Solutionकविता के आधार पर 'मनुष्यता' के गुणों/लक्षणों की चर्चा विस्तारपूर्वक कीजिए।
View Solution.0.12 मी फोकस, दूरी के उत्तल लेन्स से वस्तु का तीन गुना वास्तविक प्रतिबिम्ब पर्दे पर प्राप्त करने के लिए वस्तु को लेन्स से दूर रखना
View Solutionनिम्न के लिए हाइड्रोजनीकरण की ऊष्मा की तुलना कीजिए-
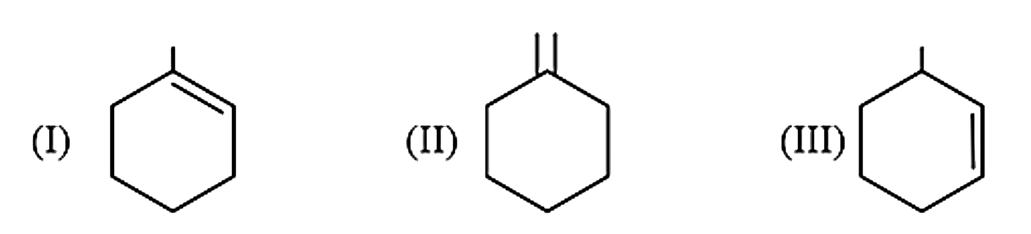
View Solutionपतले लेंस के लिये अपवर्तन सुत्र#!#लेंस की फोकस दूरी की निर्भरता
View Solutionद्रौपदी की लाज बचाने के लिए कृष्ण ने क्या किया था? मीरा के पद के आधार पर स्पष्ट कीजिए।
View Solution
