यदि प्रिज्म का कोण A बहुत छोटा है तो सिद्ध कीजिए- δm=(n−1)A, जहाँ δm न्यूनतम विचलन कोण तथा n प्रिज्म का अपवर्तनांक है |
प्रिज्म के लिए i−δ वक्र-

प्रिज्म के अपवर्तनांक के लिए सूत्र-माना ABC एक प्रिज्म का मुख्य परिच्छेद है | प्रिज्म का अपवर्तक कोण A है | माना प्रकाश की एक किरण IP, प्रिज्म के अपवर्तक पृष्ठ AB पर तिरछी आपतित होती है जो की अभिलम्ब N1PO की ओर झुकती हुए PQ दिशा में आप्वार्तित हो जाती है | इस पृष्ठ पर आपतन कोण i1 तथा अपवर्तन कोण r1 है | अपवर्तित किरण PQ, पृष्ठ AC पर अभिलम्ब N2QO से दूर हटती हुई वायु में QS दिशा में चली जाती है | इस पृष्ठ पर आपतन
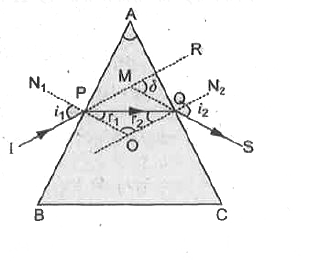
कोण r2 तथा अपवर्तन कोण i2 है | आपतित किरण IP को आगे की ओर तथा निर्गत किरण QS को पीछे की ओर बढाने पर, ये दोनों किरणे M बिंदु पर मिलती है | इन दोनों किरणों के बीच बना कोण δ ही विचलन कोण है |
ΔMPQ में δ बहिषकोण है |
अत: δ=∠RMS=∠MPQ+∠MQP
=(i1−r1)+(i2−r2)
=(i1+i2)−(r1+r2)
अल्पतम विचलन δ=δm की स्थिति में,
i1=i2=i तथा r1=r2=r [अल्पतम विचलन की शर्त]
अत: δm=2i−2r
अब चतुर्भुज APOQ में, ∠APO+∠AQO=2 समकोण [∵ प्रत्येक कोण समकोण है]
अत: शेष कोण ∠A+∠POQ=2 समकोण
परन्तु ΔPQO में, ∠POQ+∠r1+∠r2=2 समकोण
अत: ∠A+∠POQ=∠POQ+∠r1+∠r2
∠A=r1+r2=2r [∵r1=r2=r]
समीकरण (1) व् समीकरण (2) से,
δm=2i−A अथवा i=(A+δm2)
स्नेल के नियम से, प्रिज्म के पदार्थ का अप्वार्तानांक
ang=sinisinr=sin(A+δm2)sinA2
पतले प्रिज्म से उत्पन्न विचलन-जब प्रिज्म पतला हो (अर्थात A=5∘ से कम हो) तो अल्पतम विचलन δm भी बहुत छोटा होगा |
अत: sinA+δm2=A+δm2
तथा sinA2=A2 रखने पर,
n=(A+δm/2)A/2
अथवा δm=(n−1)A
Topper's Solved these Questions
Similar Questions
कांच-जल के मध्य पृष्ठ पर क्रांतिक कोण ज्ञात कीजिए यदि वायु के सापेक्ष कांच एवं जल के अवपरतणंक क्रमश: 3/2 एवं 4/3 है !
View Solutionदो समान्तर धारावाही तारों के मध्य में चुम्बकीय क्षेत्र का मान B है जबकि तारों में क्रमशः i तथा 2i धारायें बह रही है। यदि धारा i वाले टनों में धारा का मान शून्य कर दिया जाये तब चुम्बकीय क्षेत्र का मान क्या होगा?
View Solutionयदि प्रिज्म का कोण बहुत छोटा हों, तो सिध्द कीजिये δ=(μ−1)A,यहाँdeltaविचलनकोण,Aप्रिज्मकाकोणतथाmu प्रिज्म के पदार्थ का अपवर्तनांक है।
View Solutionनिम्नलिखित सर्वसमिका सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है :
cosA1+sinA+1+sinAcosA=2secA
View Solutionयदि →a.→b=0 तथा →a+→b,→b के साथ 60° का कोण बनाते हैं तो |→a| बराबर है
View Solutionएक सदिश ¯¯¯¯¯¯OA,OX से 60∘ का कोण बनाता है और OY से 45∘ का कोण बनाता है तथा ∣∣¯¯¯¯¯¯OA∣∣=10 इकाई है। बिंदु A का स्थिति सदिश ज्ञात कीजिए।
View Solutionयदि xy = 4 तथा x> 0 तो x का वह मान ज्ञात कीजिए जिसके लिए x + y न्यूनतम है।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionएक रेखा x- अक्ष से 120∘ तथा y-अक्ष से 60∘ का कोण बनाती है, तो रेखा द्वारा z-अक्ष से बना कोण ज्ञात कीजिए।
View Solutionयदि sinθ=12 तथा θ एक अधिक कोण है , तो cotθ का मान होगा
View Solutionयदि a तथा b इकाई सदिश हैं तथा θ इनके बीच का कोण है। तब ∣∣ˆa+ˆb∣∣<1 यदि
View Solutionप्रिज्म तथा प्रिज्म द्वारा प्रकाश का अपवर्तन|प्रिज्म के पदार्थ का अपवर्तनांक तथा विचलन#!#महत्वपूर्ण प्रश्न
View Solutionप्रकाश का अपवर्तन|विभिन्न माध्यमों का अपवर्तनांक#!#क्रांतिक कोण तथा पूर्ण आंतरिक परावर्तन
View SolutionIf N= 0.369369369... and M = 0.531531531531..., then what is the value of (1N)+(1M)?
यदि N = 0.369369369... और M = 0.531531531531...,है, (1N)+(1M) तो का मान क्या है?
View Solution
