दो सदिशों →A तथा →B के परिमाण बराबर है (→A+→B) का परिमाण (→A−→B) के परिमाण का n गुना है। →A तथा →B के बीच कोण है
sin−1[n2−1n2+1]
cos−1[n−1n+1]
cos−1[n2−1n2+1]
sin−1[n−1n+1]
The correct Answer is:C
A2+A2+2ABcosθ=n2(A2+A2−2ABcosθ)
A2+A2+2A2cosθ=n2(A2+A2−2A2cosθ)
2A2(1+cosθ)=2A2n2(1−osθ)k
1+cosθ=n2−n2cosθ
cosθ(1+n2)=n2−1
cosθ=n2−1n2+1
θ=cos−1(n2−1n2+1)
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - JEE SECTION8videos
गणितीय अवधाराणाएं एवं सदिश
- BOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - ASSERTION & REASON15videos
गणितीय अवधाराणाएं एवं सदिश
- BOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - Ordinary Thinking ( लामी प्रमेय)3videos
गणितीय अवधाराणाएं एवं सदिश
- BOOK - ERRORLESS HINDICHAPTER - किरण प्रकाशिकीEXERCISE - Self Evaluation Test (किरण प्रकाशिकी)26videos
किरण प्रकाशिकी
- BOOK - ERRORLESS HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - Self Evalution Test17videos
गुरुत्वाकर्षण
Similar Questions
दो सदिश →A=3ˆi+4ˆj तथा →B=ˆi+ˆj दिए गए हैं →A तथा →B के मध्य कोण θ है। निम्न में से कौन सा कथन सही है
04:08View Solutionप्रक्कथनः →A×→B सदिशों →A+→B व →A−→B दोनों पर लम्बवत होता है।
कारणः →A+→B तथा →A−→B उस समतल में स्थित होते हैं जिसमें →A तथा →B दोनो स्थित है किंतु →A×→B उस समतल के लम्बवत होता है जिसमें →A तथा →B दोनों स्थित है।02:31View Solutionतीन समतलीय सदिश P,Q तथा R किसी बिंदु पर कार्यरत है तथा सामयवस्था में है। दिया है P=1.9318 किग्रा भार sinθ1=0.9659 तो R का मान (किग्रा. भार में) है
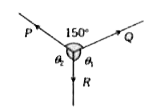 02:47View Solution
02:47View Solutionएक खगोलीय दूरदर्शी में सामान्य संजन की स्थिति में, अभिदृश्यक पर एक L लम्बाई की सीधी काली रेखा खींची गई है | नेत्रिका इस रेखा का वास्तविक प्रतिबिम्ब बनाता है | प्रतिबिम्ब की लम्बाई l है | तब दूरदर्शी की आवर्धन क्षमता है
04:23View Solutionपृथ्वी की सूर्य के चारों ओर परिक्रमण कक्ष की माध्य त्रिज्या 1.5×1011 मीटर है। बुध की सूर्य के चारों ओर परिक्रमण कक्ष की माध्य त्रिज्या 6×1010 मीटर है। बुध सूर्य का चक्कर लगाएगा
02:12View Solutionयदि ∣∣→a+→b∣∣=∣∣→a−→b∣∣ , तब दिखाइये कि सदिश →aतथा →b लम्बवत है |
03:16View Solutionयदि →a=(5ˆi−ˆj−3ˆk)तथा →b=(ˆi+3ˆj−5ˆk) तब सिद्ध कीजिए कि →a+→bतथा →a−→b लम्बवत है |
03:24View Solutionयदि →a,→b,→c तीन असमतलीय एकांक सदिश है तथा →a×(→c×→b)=→b+→c√2 तो →a और →b के मध्य कोण है -
05:16View Solutionयदि →a=4ˆi+3ˆj तथा →b=3ˆi+ˆj हो, तो निम्नलिखित के परिमाण बताएँ।
(a)→a,(b)→b,(c)→a+→bतथा(d)→a−→b.04:32View Solutionयदि →a और →b असंरेख है ,तो x का मान ज्ञात कीजिए| जिसके लिए सदिश α=(2x+1)→a−→b और β=(x−2)→a+→b संरेख है
02:39View Solutionयदि →a.→b=0 तथा →a+→b,→b के साथ 60° का कोण बनाते हैं तो |→a| बराबर है
04:23View Solutionयदि →a+→b+→c=0 तो सिद्ध कीजिए कि →a×→b=→b×→c=→c×→a इस परिमाण का ज्यामितीय विमोचन कीजिए |
04:32View Solutionयदि [→a×→b→b×→c→c×→a]=λ[→a→b→c]2 तो λ बराबर है |
02:39View Solution→a,→b,→c क्रमश 3,4,5 परिमाण के सदिश है। यदि प्रत्येक सदिश अन्य दो सदिशो के योग पर लम्ब हो, तो सदिश →a+→b+→c का परिमाण ज्ञात किजिए।
04:32View Solutionयदि दो सदिश →a और →b इस प्रकार है कि |→a|=2,∣∣→b∣∣=3 और →a⋅→b=4 तो ∣∣→a−→b∣∣ ज्ञात किजिए।
02:59View Solutionयदि →a,→b,→c समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश →a+→b+→c सदिशों →a,→b और →c के साथ बराबर कोण बनाता है।
03:32View Solution

