दो सदिशों →P व →Q का परिणामी →R है। यदि →Q का परिमाण दुगुना कर दिया जाये तब नया परिणामी →P के लम्बवत हो जाता है तब →R का परिमाण होगा
P+Q
Q
P
P+Q2
The correct Answer is:B
→P+→Q=→R
tanα=QsinθP+Qcosθ
जब Q को दुगुना किया जाता है तब
परिणामी →P के लम्बवत हो जाता है
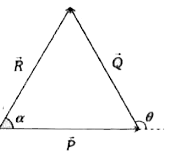
∴R2=P2+Q2+2PQcosθ…………..i
R21=P2+4Q2+4PQcosθ ………….ii
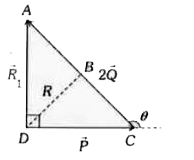
समकोण त्रिभुज ADC से
4Q2=R21+P2
R21=4Q2−P2
(ii) में मान रखकर हल करने पर
P2+2PQcosθ=0 ………ii
(i) में (iii) से मान रखने पर R=Q
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - JEE SECTION8videos
गणितीय अवधाराणाएं एवं सदिश
- BOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - ASSERTION & REASON15videos
गणितीय अवधाराणाएं एवं सदिश
- BOOK - ERRORLESS HINDICHAPTER - गणितीय अवधाराणाएं एवं सदिशEXERCISE - Ordinary Thinking ( लामी प्रमेय)3videos
गणितीय अवधाराणाएं एवं सदिश
- BOOK - ERRORLESS HINDICHAPTER - किरण प्रकाशिकीEXERCISE - Self Evaluation Test (किरण प्रकाशिकी)26videos
किरण प्रकाशिकी
- BOOK - ERRORLESS HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - Self Evalution Test17videos
गुरुत्वाकर्षण
Similar Questions
दो सदिश →A=3ˆi+4ˆj तथा →B=ˆi+ˆj दिए गए हैं →A तथा →B के मध्य कोण θ है। निम्न में से कौन सा कथन सही है
01:45View Solutionप्रक्कथनः →A×→B सदिशों →A+→B व →A−→B दोनों पर लम्बवत होता है।
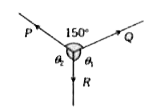
कारणः →A+→B तथा →A−→B उस समतल में स्थित होते हैं जिसमें →A तथा →B दोनो स्थित है किंतु →A×→B उस समतल के लम्बवत होता है जिसमें →A तथा →B दोनों स्थित है।View Solutionतीन समतलीय सदिश P,Q तथा R किसी बिंदु पर कार्यरत है तथा सामयवस्था में है। दिया है P=1.9318 किग्रा भार sinθ1=0.9659 तो R का मान (किग्रा. भार में) है
 View Solution
View Solutionएक खगोलीय दूरदर्शी में सामान्य संजन की स्थिति में, अभिदृश्यक पर एक L लम्बाई की सीधी काली रेखा खींची गई है | नेत्रिका इस रेखा का वास्तविक प्रतिबिम्ब बनाता है | प्रतिबिम्ब की लम्बाई l है | तब दूरदर्शी की आवर्धन क्षमता है
03:32View Solutionपृथ्वी की सूर्य के चारों ओर परिक्रमण कक्ष की माध्य त्रिज्या 1.5×1011 मीटर है। बुध की सूर्य के चारों ओर परिक्रमण कक्ष की माध्य त्रिज्या 6×1010 मीटर है। बुध सूर्य का चक्कर लगाएगा
02:49View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
02:56View SolutionThree vectors →P,→Q and →R such that ∣∣→Q∣∣=A√2 and the angles between →P and →Q,→Q and →R,→R and →P are 90∘,150∘,120∘ respectivlely. Find the value of ∣∣→P∣∣=
View SolutionMagnitudes of vectors →P,→Q and →R are equal, If →P+→Q+→R=0, then angle between →Rand→Q is α while if →P+→Q=→R, the angle between →R and →P is β, then :
03:21View SolutionIf vecP+vecQ=vecR" & "vecR is perpendicular to vecP . define angle between vecP" & "vecQ" if " vec|P|=vec|R|-
03:27View SolutionIf vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
03:12View SolutionThe sum of two forces vecP and vecQ is vecR such that |vecR|=|vecP| . The angle theta (in degrees) that the resultant of 2vecP and vecQ will make with vecQ is , _____________.
02:28View Solutionतीन सदिश →q,→p और →r के लिए [→p,→q→r]=(→p×→q).→r=→p.(→q×→r) है फिर →p,→q→r एकटालिय होने पर [→p→q→r]=0.
[2→a−2→b−→c−2→c−→a]=02:22View Solutionतीन सदिश →q,→p और →r के लिए [→p,→q→r]=(→p×→q).→r=→p.(→q×→r) है फिर →p,→q→r एकटालिय होने पर [→p→q→r]=0.
माना कि →V=2ˆi+ˆj−ˆk और →W=ˆi+3ˆkयदि →U इकाई सदिश हो, तो [→U→V→W]का महत्तम मान होगा04:28View SolutionLet →qand→r be non - collinear vectors, If →p is a vector such that →p.(→q+→r)=4and→p×(→q×→r)=(x2−2x+9)→q then +(siny)→r
(x, y) lies on the line02:06View SolutionIf vecP+vecQ=vecR and |vecP|=|vecQ|=sqrt(3) and |vecR|=3 , then the angle between vecP and vecQ is
14:24View SolutionThe resultant of vecP and vecQ is vecR . The angle between vecP and vecQ is
02:54View Solution

