ऊर्ध्वाधर धुरी पर दो चकती A तथा B को समाक्ष रूप से लगाया गया है। चकती के जड़त्व आघूर्ण, उभयनिष्ठ अक्ष के परितः क्रमशः I तथा 21 है। स्प्रिंग को x1 दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग 2ω प्राप्त करती है। समान स्प्रिंग नियतांक की स्प्रिंग को x2 दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग ω प्राप्त करती है। दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है।
जब चकती B को चकती A के सम्पर्क में किया जाता है, तब वे समय में उभयनिष्ठ कोणीय वेग प्राप्त कर लेती है। इस समय अन्तराल में एक चकती द्वारा दूसरी से प्राप्त औसत घर्षण बल आघूर्ण है
Iω24
9Iω2t
9Iω4x
3Iω2t
The correct Answer is:A
कोणीय संवेग संरक्षण से, (I)(2ω)+(2I)(ω)=(I+2I).ωf
ωf=(4ω3)
समय t के लिये औसत घर्षण बल आघूर्ण (τ) क्रियाशील होता है, तब ω का मान ωf तक परिवर्तित होगा तहत कोणीय आवेग प्रत्येक चकती को विपरीत रूप में प्राप्त होता है।
अतः ω1=ω+τ2It
∴4ω3=ω+τ2It
τ=2Iω3t
∵ कोणीय आवेग =τ.t⇒τ=ΔLt=l.(2ω)−I(4ω3)t
अतः घर्षण बल आघूर्ण, τ=2lω3t.
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - ASSERTION & REASON
25 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - SELF EVALUATION TEST
16 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - GRAPHICAL QUESTIONS
6 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
प्रक्कथन : दो कणों के निकाय का द्रव्यमान-केंन्द्र दोनों कणोको जोड़ने वाली रेखा पर स्थित होता है, तथा भारी कण के समीप होता है।
कारण : किसी कण के द्रव्यमान तथा द्रव्यमान केंद्र से इसकी दूरी का गुणनफल दूसरे कण के द्रव्यमान तथा द्रव्यमान केंद्र की दूरी के गुणनफल के आंकिक मान के बराबर होता है।
View Solution5×10−3kgm2 जड़त्व आघूर्ण का एक पहिया 20 चक्कर/सैकण्ड की दर से घूर्णन गति कर रहा है। इसे 20 सैकण्ड में विरामावस्था में लाने के लिये आवश्यक कोणीय मंदन का मान होगा
View Solutionएक जेट इंजन के परीक्षण के दौरान, उसका संपीडक (Compressor) निम्न ग्राफ के अनुसार चक्रण करता है। परीक्षण के दौरान संपीडक द्वारा पूर्ण किये गये चक्करों की संख्या होगी
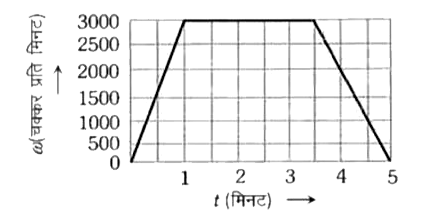
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionदरअसल शुरू से ही था हमारे आदेशों में कही एक जानी दुश्मन कि घर को बचाना है लूटेरों से शहर को बचाना है नदियों से देश को बचाना है , देश के दुश्मनों से बचाना है - नदियों को नाला हो जाने से हवा को धुआँ हो जाने से खाने को जहर हो जाने से : बचाना है - जंगल को मरुस्थल हो जाने से , बचाना है - मनुष्य को , जंगल हो जाने से । शब्द - सारिणी की सहायता से समान अर्थ के शब्द ढूढ़कर लीखिए :
View Solutionउन सरल रेखाओ के समीकरण ज्ञात कीजिए जो :
x=3 तथा x=−3 से समान दूरी पर है
View Solutionउन सरल रेखाओ के समीकरण ज्ञात कीजिए जो :
y=−5 तथा y=1 से समान दूरी पर है
View Solutionएक व्दिपरमाणुक अणु m_(1) "तथा" m_(2) के दो द्रव्यमानों से बना है जो कि दूरी r पर है । यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकर हम इसकी घूर्णन ऊर्जा की गणना करें , तब इसकी ऊर्जा दी जाएगी (n एक पूर्णाक है )
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionसमीकरण y=Acosωt+Bsinωt से A तथा B को विलोपित करने पर प्राप्त होने वाला अवकल समीकरण है
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solution.0.12 मी फोकस, दूरी के उत्तल लेन्स से वस्तु का तीन गुना वास्तविक प्रतिबिम्ब पर्दे पर प्राप्त करने के लिए वस्तु को लेन्स से दूर रखना
View Solution(-1-1) और (4, 2) से समान दूरी पर स्थित बिन्दुओं के बिन्दुपथ का समीकरण है
View SolutionRevision|किसी ऊँचाई से, यदि वस्तु ऊर्ध्वाधर नीचे की ओर कुछ प्रारम्भिक वेग से फेंकी जाये |गति के समीकरण |किसी ऊँचाई से यदि किसी वस्तु को गिराया जाये (प्रारम्भिक वेग शून्य)|किसी ऊँचाई से, यदि वस्तु ऊर्ध्वाधर ऊपर की ओर कुछ प्रारम्भिक वेग से फेंकी जाये |वस्तु की वायु की उपस्थिति मे गति |प्रश्न |OMR|Summary
View Solutionपदार्थ A और B के बीच अभिक्रिया को निम्न प्रकार दर्शाया गया है
A+B−→C इस अभिक्रिया की दर से निम्न प्रेक्षणों को प्राप्त किया जाता है

View Solution
