एक निर्देश तंत्र जो एक जड़त्वीय निर्देश तंत्र की तुलना में त्वरित हो, अजड़त्वीय निर्देश तंत्र कहलाता है। स्थिर कोणीय वेग ω से घूमती हुई डिस्क पर बद्ध निर्देश तंत्र अजड़त्वीय तंत्र का एक उदाहरण है। m द्रव्यमान का एक कण घूमती हुई डिस्क पर गतिमान है। गतिमान कण डिस्क पर बद्ध निर्देश तंत्र के सापेक्ष बल Frot तथा एक जड़त्वीय निर्देश तंत्र के सापेक्ष बल →Fln को महसूस करता है। →Frot और →Fln के बीच का संबंध निम्नलिखित समीकरण में दिया गया है →Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
यहाँ पर →vrot घूमते हुए निर्देश तंत्र में कण का वेग है तथा । कण का डिस्क के मध्य बिन्दु के सापेक्ष स्थिति सदिश है।
माना कि R त्रिज्या की एक डिस्क, जिसमें व्यास के समानान्तर एक घर्षणरहित खाँचा है, एक स्थिर काणीय गति ω से अपने अक्ष पर वामावर्त दिशा में घूम रही है। एक निर्देश तंत्र मानिए जिसका मूलबिंदु डिस्क के मध्य बिन्दु पर है एवं x-अक्ष खाँचे के समानान्तर है, z-अक्ष खाँचे के अभिलम्ब पर है एवं -अक्ष घूमने वाली अक्ष के समानान्तर है (→ω=ωˆk)lm द्रव्यमान वाले एक छोटे गुटके को समय t=0 पर →r=(R/2)ˆi बिन्दु पर धीरे से इस तरह रखा जाता है कि वो सिर्फ खाँचे में ही चल सके।
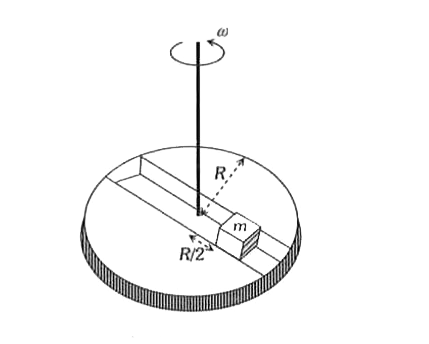
समय । पर गुटके की दूरी का मान है
R4(e2ωt+e−2ωl)
R2cos2ωt
R2cosωt
R2(eωt+e−ωt)
The correct Answer is:D
vdvdr=ω2r, जहाँ v गुटके का ऊपर की तरफ वेग है।
∫v0vdv=ω2∫rr/2rad
⇒v=ω√r2−R24
∫rR/2dr√r2−R24=ω∫t0dt
r=R4(eωt−e−ωt)
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - ASSERTION & REASON
25 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - SELF EVALUATION TEST
16 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - GRAPHICAL QUESTIONS
6 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
प्रक्कथन : दो कणों के निकाय का द्रव्यमान-केंन्द्र दोनों कणोको जोड़ने वाली रेखा पर स्थित होता है, तथा भारी कण के समीप होता है।
कारण : किसी कण के द्रव्यमान तथा द्रव्यमान केंद्र से इसकी दूरी का गुणनफल दूसरे कण के द्रव्यमान तथा द्रव्यमान केंद्र की दूरी के गुणनफल के आंकिक मान के बराबर होता है।
View Solution5×10−3kgm2 जड़त्व आघूर्ण का एक पहिया 20 चक्कर/सैकण्ड की दर से घूर्णन गति कर रहा है। इसे 20 सैकण्ड में विरामावस्था में लाने के लिये आवश्यक कोणीय मंदन का मान होगा
View Solutionएक जेट इंजन के परीक्षण के दौरान, उसका संपीडक (Compressor) निम्न ग्राफ के अनुसार चक्रण करता है। परीक्षण के दौरान संपीडक द्वारा पूर्ण किये गये चक्करों की संख्या होगी
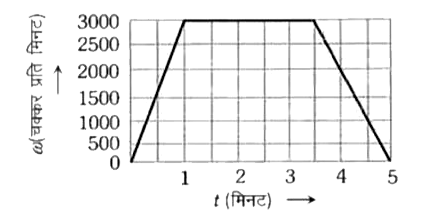
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionगति का वर्णन || निर्देश तंत्र || सरल रेखीय गति || एकसमान गति और असमान गति || दूरी || विस्थापन ||
View Solutionअरस्तू की भ्रामकता | जड़त्व, द्रव्यमान तथा भार | निर्देश तंत्र
View Solutionगति का वर्णन || निर्देश तंत्र || सरल रेखीय गति || दूरी || विस्थापन ||
View Solutionअरस्तू की भ्रामकता || जड़त्व, द्रव्यमान तथा भार || निर्देश तंत्र
View Solutionगति का वर्णन | निर्देश तंत्र | सरल रेखीय गति | एकसमान गति
View Solutionमानव श्वसन तंत्र एक ही क्लास में
View Solutionनिर्देश तंत्र | गति एवं विराम | महत्वपूर्ण प्रश्न
View Solutionदूरी एवं विस्थापन |निर्देश तंत्र #!#गति एवं विराम
View Solutionनिर्देश तंत्र |सरल रेखीय गति #!#दूरी एवं विस्थापन #!#एकसमान गति
View Solutionशरीर द्रव्यों का परिसंचरण | रक्त परिसंचरण के प्रकार | खुला परिसंचरण तंत्र | बंद परिसंचरण तंत्र | लसिका तंत्र
View Solutionपरिचय | विभिन्न जीवों में तंत्रिका तंत्र | तंत्रिका तंत्र के प्रकार
View Solution
