एक अवितान्य डोरी से जुडा हुआ M द्रव्यमान का एक कण स्थिर बिन्दु 0 के परितः R त्रिज्या के ऊर्ध्वाधर वृत्त में गति कर रहा हैं। यह चित्रानुसार निम्नतम स्थिति पर क्षैतिज दिशा में वेगu आरोपित करता हैं। निम्न जानकारी दी गई हैं (i)
h ऊँचाई पर वेग सूत्र u2=u2−2gh के प्रयोग से ज्ञात किया जा सकता है
(ii) कण वृत्त को पूर्ण करेगा यदि μ≥√5gR
(iii) कण निचले अर्धभाग (0∘<θ<90∘) में दोलन करेगा यदि 0<u≤√2gR
(iv) ‘h’ ऊँचाई पर तनाव का परिमाण सूत्र T=MR{u2+gR−3gh) के प्रयोग से ज्ञात किया जाता है
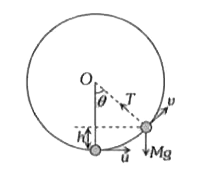
यदि M=2kg, R=2m तथा u=10m/s कण का वेग जब θ=60∘
2√5m/s
4√5m/s
5√2m/s
5m/s
The correct Answer is:B
θ=60∘ पर, h=R−Rcos60∘=R2
v2=u2−2gh में h=R2 रखने पर, हमें परिणाम मिलते है।
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - ASSERTION & REASON
25 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - SELF EVALUATION TEST
16 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - GRAPHICAL QUESTIONS
6 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
प्रक्कथन : दो कणों के निकाय का द्रव्यमान-केंन्द्र दोनों कणोको जोड़ने वाली रेखा पर स्थित होता है, तथा भारी कण के समीप होता है।
कारण : किसी कण के द्रव्यमान तथा द्रव्यमान केंद्र से इसकी दूरी का गुणनफल दूसरे कण के द्रव्यमान तथा द्रव्यमान केंद्र की दूरी के गुणनफल के आंकिक मान के बराबर होता है।
View Solution5×10−3kgm2 जड़त्व आघूर्ण का एक पहिया 20 चक्कर/सैकण्ड की दर से घूर्णन गति कर रहा है। इसे 20 सैकण्ड में विरामावस्था में लाने के लिये आवश्यक कोणीय मंदन का मान होगा
View Solutionएक जेट इंजन के परीक्षण के दौरान, उसका संपीडक (Compressor) निम्न ग्राफ के अनुसार चक्रण करता है। परीक्षण के दौरान संपीडक द्वारा पूर्ण किये गये चक्करों की संख्या होगी
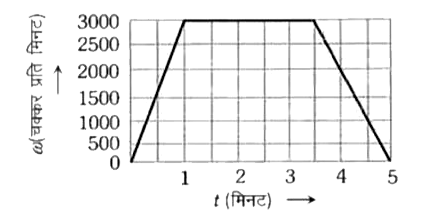
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionबिन्दु (1, 2) से दीर्घवृत्त 3x2+2y2=5 पर खींची गई स्पर्शी युग्मों के बीच का कण है
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionआकृति में, वृत्त के छायांकित भाग को कहते हैं:
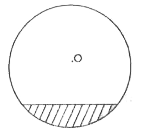
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solution
