नीचे दी गयी सूची-1 में, एक कण के चार विभिन्न पथ, समय के विभिन्न फलनों (functions) के रूप में दिये गये हैं। इन फलनों में α और β उचित विमाओं वाले धनात्मक नियतांक (positive constants) हैं, जहाँ α≠β । प्रत्येक पथ में कण पर लगने वाला बल या तो शून्य है या संरक्षी (conservative) है। सूची-II में कण की पाँच भौतिक राशियों का विवरण दिया गया है: →p रेखीय संवेग (linear momentum) है,→L मूल बिंदु (origin) के सापेक्ष कोणीय संवेग (angular momentum) है,Kगतिज ऊर्जा (kinetic energy) है, U स्थितिज ऊर्जा (potential energy) है और E कुल ऊर्जा (total energy) है। सूची-1 के प्रत्येक पथ का सूची-II में दिये गये उन राशियों से सुमेल कीजिये, जो उस पथ के लिए संरक्षी (conserved) हैं।
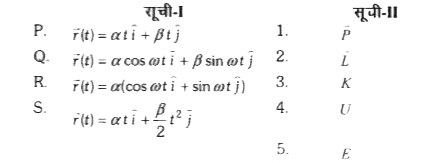
The correct Answer is:P→1,2,3,4,5;Q→2,5;R2,3,4,5;S→5
(P)→r(t)=αtˆi+βtˆj
→v=d→r(t)dt=αˆi+βˆj {नियत}
→a=→dvdt=0
→P=m→v (नियत)
k=12mv2{नियत}
→F=−∂U∂xˆi+∂U∂yˆi]=0
⇒U→
K=K+U
d→Ldt=→τ=→r×→F=0
→L= नियत
(Q)→r=αcos(ωt)ˆi+βsin(ωt)ˆj
→v=d→rdt=0αωsin(ωt)ˆi+βωcos(ωt)ahtj
→a=d→vdt=−αω2cos(ωt)ˆi−βω2sin(ωt)ˆj
=−ω2[αcos(ωt)ˆi+βsin(ωt)ˆj]
→a=−ω2→r
→τ=→r×→F=0{→r→F समान्तर ह}
ΔU=−∫→F.dr=+∫r0mω2.r.dr
ΔU=mω2[r22]
U∝r2
r=√α2cos2(ωt)+β2sin2(ωt)
r फलन का (t ) का U निर्भर करता है r पर अतः यह समय परिवर्ती है। कुल ऊर्जा सदैव नियत रहेगी क्योकि बल नियत है।
(R)→r(t)=α(cosωˆi+sin(ωt)ˆj)
→v(t)=→dr(t)dt=α[−ωsin(ωt)ˆi+ωcos(ωt)ˆj]
|→v|=αω चाल नियत रहेगी
→a(t)=d→v(t)dt=α[−ω2cos(ωt)ˆi−ω2sin(ωt)ˆj]
=−αω2[cos(ωt)ˆi+sin(ωt)ˆj]
→a(t)=−ω2(→r)
→τ=→F×→r=0
|→r|=α (नियत है)
बल केंद्रीय प्रकृति का है तथा स्थिर बिंदु से दुरी नियत है। स्थितिज ऊर्जा नियत ह। गतिज ऊर्जा भी नियत है (चाल नियत है)।
(S)→r=αtˆi+β2t2ˆj
→v=d→rdt=αˆi+βtˆj (कण की चाल t पर निर्भर है)
→ad→vdt=βˆj {नियत}
→F=m→a {नियत}
ΔU=−∫→F.d→r=−m∫t0βˆj.(αˆi+βtˆj)dt
U=−mβ2t22
k=12mv2=12m(α2+β2t2)
E=k+U=12mα2 [नियत]
Topper's Solved these Questions
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - ASSERTION & REASON
25 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - SELF EVALUATION TEST
16 Videos
- घूर्णी गति BOOK - ERRORLESS HINDICHAPTER - घूर्णी गति EXERCISE - GRAPHICAL QUESTIONS
6 Videos
- घर्षण BOOK - ERRORLESS HINDICHAPTER - घर्षण EXERCISE - SELF EVALUATION TEST
11 Videos
- चुम्बकत्व BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test
15 Videos
Similar Questions
प्रक्कथन : दो कणों के निकाय का द्रव्यमान-केंन्द्र दोनों कणोको जोड़ने वाली रेखा पर स्थित होता है, तथा भारी कण के समीप होता है।
कारण : किसी कण के द्रव्यमान तथा द्रव्यमान केंद्र से इसकी दूरी का गुणनफल दूसरे कण के द्रव्यमान तथा द्रव्यमान केंद्र की दूरी के गुणनफल के आंकिक मान के बराबर होता है।
View Solution5×10−3kgm2 जड़त्व आघूर्ण का एक पहिया 20 चक्कर/सैकण्ड की दर से घूर्णन गति कर रहा है। इसे 20 सैकण्ड में विरामावस्था में लाने के लिये आवश्यक कोणीय मंदन का मान होगा
View Solutionएक जेट इंजन के परीक्षण के दौरान, उसका संपीडक (Compressor) निम्न ग्राफ के अनुसार चक्रण करता है। परीक्षण के दौरान संपीडक द्वारा पूर्ण किये गये चक्करों की संख्या होगी
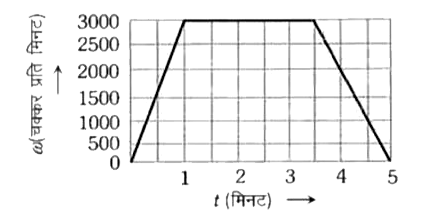
View Solutionयदि 19.6 न्यूटन का बल किसी 10 किग्रा के पिण्ड पर लगया जाता है तल के समांतर इस पिण्ड 5 किग्रा का द्रिव्यमान रख दिया जाए तो सतह के समांतर संयुक्त वस्तु को गति करने के लिए आरोपित बल का मान होगा
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा

View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionएक कण पर लगे समान परिमाण वाले तीन बल संतुलन में हैं, तो उनके बीच व कोण _____ होगा।
View Solutionफलनों के प्राचलिक रूप में अवकलज | उदाहरण
View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए:
अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए।
गद्यांश में लेखक ने किन बातों में उलझे रहने की बात कही है?
View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए: अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए। आशय स्पष्ट कीजिए : असल में दोनों काल मिथ्या हैं।
View Solutionनिम्नलिखित गद्यांश को ध्यानपूर्वक पढ़कर पूछे गए प्रश्नों के उत्तर लिखिए:
अकसर हम या तो गुजरे हुए दिनों की खट्टी-मीठी यादों में उलझे रहते हैं या भविष्य के रंगीन सपने देखते हैं। हम या तो भूतकाल में रहते हैं या भविष्यकाल । असल में दोनों काल मिथ्या हैं। एक चला गया है, दूसरा आया नहीं है। हमारे सामने जो वर्तमान क्षण है, वही सत्य है। उसी में जीना चाहिए।
लेखक ने सत्य किसे कहा है और क्यों?
View Solutionपत्रकारिता के विभिन्न आयामों में से एक है
View Solutionराजस्थान में वर्षा की मात्रा नापने में इंच या सेंटीमीटर के स्थान पर किस शब्द का प्रयोग होता है ?
View Solutionपत्रकारिता के विभिन्न आयामों में से एक है
View Solutionभोजन के रूप में पौधों के विभिन्न प्रकार
View Solution
