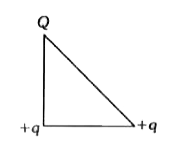
दिखाये गये समीकरणीय समद्विबाहु त्रिभुज के कोनों पर तीन आवेश Q, +q तथा +q रखे गये हैं | इस विन्यास की कुल विद्युत स्थैतिक ऊर्जा शून्य होगी यदि Q का मान है
−√2q√2+1
−2q
−q1+√2
+q
The correct Answer is:A
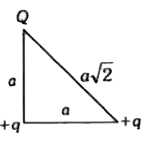
U=K[q2a+Qqa+Qqa√2]=0
⇒q=−Q[1+1√2]⇒Q=−q√2√2+1
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Graphical Questions13videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - JEE Section (More than one correct answers)17videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Ordinary Thinking (संधरित्रों का संयोजन)91videos
स्थिर वैद्युत
- BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Self Evaluation Test (सरल आवर्त गति )19videos
सरल आवर्त गति
Similar Questions
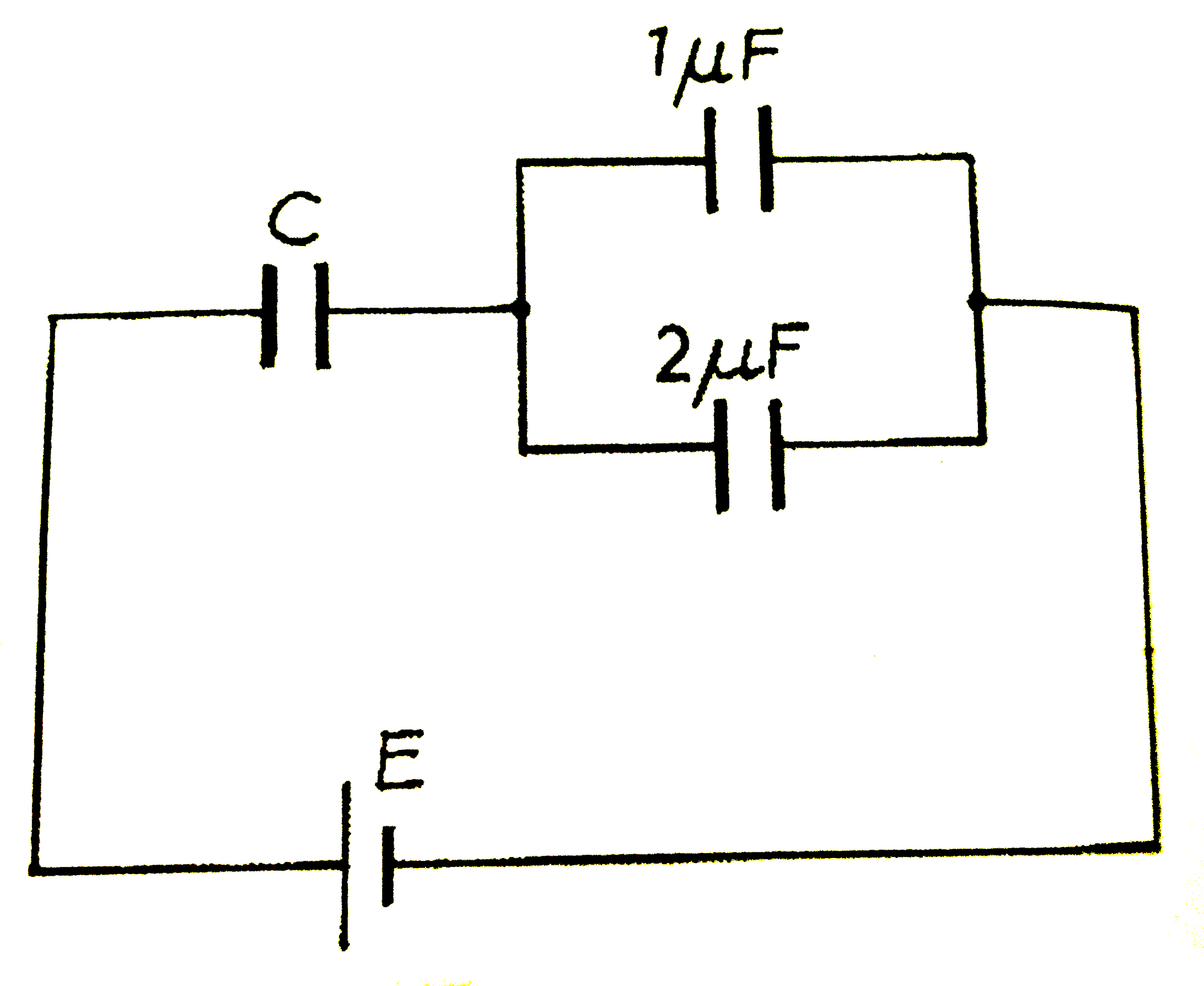
दिए गये परिपथ में, C के मान के 1μF से 3μF परिवर्तित होने से, 2μF संधारित्र पर आवेश Q2 में परिवर्तन होता है। के पहलन के रूप में Q2 को कौन-सा आलेख सही दर्शाता है? (आलेख केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है।)
 03:54View Solution
03:54View Solutionविद्युत क्षेत्र की तीव्रता का मात्रक एवं विमा लिखिए
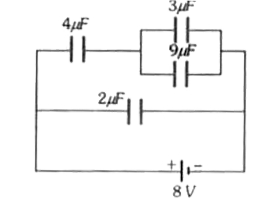
03:50View Solutionसंधारित्रों से बने एक परिपथ को चित्र में दिखाया गया है| एक बिन्दु - आवेश Q ( जिसका मान 4μF तथा 9μF वाले संधारित्रों के कुल आवेशों के बराबर है ), के द्वारा 30m दूरी पर वैद्युत-क्षेत्र का परिमाण होगा
 02:42View Solution
02:42View Solutionएक सरल लोलक , का गोलक एक धात्विक खोकला गोला है। इसका आवर्तकाल T है। जब गोलक में रेत भरी है। तब आवर्तकाल T1 है जब यह मरकरी से भरा है तब आवर्तकाल T2 है जब यह मरकरी से आधा भरा है तब इसका आवर्तकाल T3 है । तब निम्न में से सही विकल्प है।
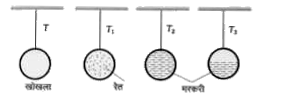 04:39View Solution
04:39View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
04:35View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
04:32View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
03:50View Solution△ABC के अन्तरगर्त वृत्त का केंद्र O है तथा भुजा AB,BC,CA क्रमशः वृत्त को बिंदु P, Q, R पर स्पर्श करती है। यदि ∠POQ=110∘,∠QOR=120∘ है ,तो ∠CAB का मान है -
04:38View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
03:13View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
03:43View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
04:30View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
34:13View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
34:41View Solutionयदि →a=(1,p,1),→b=(q,2,2),→a.→b=r तथा →a×→b=(0,+3,-3) , तब p,q,r के मान क्रमश: हैं
05:04View Solution1 किग्रा, (32) किग्रा, एवं 2 किग्रा द्रव्यमानों के तीन कण a भुजा वाले एक समबाहु त्रिभुज के शीर्षों पर रखे गये हैं। द्रव्यमान केन्द्र के X, Y निर्देशांक होंगे-
03:24View SolutionL√L, L√Q, Q√L तथा Q√Q के व्युत्क्रमों का समाकलन
01:52View Solution

