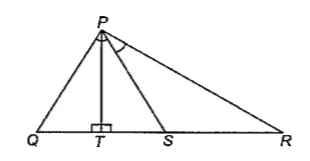
In △PQR,∠Q≻∠R, PS is
the bisector of ∠P and PT⊥QR.
If ∠SPT=28∘ and ∠R=23∘ ,
then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा
PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
74∘
79∘
82∘
89∘
To solve the problem, we will follow these steps:
Step 1: Understand the triangle and given information
We have triangle PQR where angle Q is greater than angle R. PS is the bisector of angle P, and PT is perpendicular to QR. We know:
- Angle SPT = 28°
- Angle R = 23°
Step 2: Set up the triangle and angles
Since PT is perpendicular to QR, we have:
- Angle PRT = 90°
Step 3: Calculate angle RPT
Using the angle sum property in triangle RPT:
Angle RPT+Angle PRT+Angle R=180°
Substituting the known values:
Angle RPT+90°+23°=180°
Angle RPT+113°=180°
Angle RPT=180°−113°=67°
Step 4: Calculate angle PST
Now, we can find angle PST using the angles in triangle SPT:
Angle SPT+Angle PST+Angle RPT=180°
Substituting the known values:
28°+Angle PST+67°=180°
Angle PST+95°=180°
Angle PST=180°−95°=85°
Step 5: Find angle P
Since PS is the bisector of angle P, we have:
Angle P=2×Angle PST=2×39°=78°
Step 6: Calculate angle Q
Now we can find angle Q using the angle sum property in triangle PQR:
Angle P+Angle Q+Angle R=180°
Substituting the known values:
78°+Angle Q+23°=180°
Angle Q+101°=180°
Angle Q=180°−101°=79°
Final Answer
The measure of angle Q is 79°.
---
We have triangle PQR where angle Q is greater than angle R. PS is the bisector of angle P, and PT is perpendicular to QR. We know:
- Angle SPT = 28°
- Angle R = 23°
Since PT is perpendicular to QR, we have:
- Angle PRT = 90°
Using the angle sum property in triangle RPT:
Angle RPT+Angle PRT+Angle R=180°
Substituting the known values:
Angle RPT+90°+23°=180°
Angle RPT+113°=180°
Angle RPT=180°−113°=67°
Now, we can find angle PST using the angles in triangle SPT:
Angle SPT+Angle PST+Angle RPT=180°
Substituting the known values:
28°+Angle PST+67°=180°
Angle PST+95°=180°
Angle PST=180°−95°=85°
Since PS is the bisector of angle P, we have:
Angle P=2×Angle PST=2×39°=78°
Now we can find angle Q using the angle sum property in triangle PQR:
Angle P+Angle Q+Angle R=180°
Substituting the known values:
78°+Angle Q+23°=180°
Angle Q+101°=180°
Angle Q=180°−101°=79°
The measure of angle Q is 79°.
Topper's Solved these Questions
Similar Questions
In a quadrilateral ABCD, the bisectors of ∠C and ∠D meet at E. If ∠CED=56∘ and ∠A=49∘ , then the measure of ∠B is:
एक चतुर्भुज ABCD में, कोण C तथा कोण D के समद्विभाजक E पर मिलते हैं | यदि ∠CED=56∘ और ∠A=49∘ है, तो कोण B का मान क्या होगा ?
View SolutionIn △ABC ,AD is perpendicular to BC at D and AE is the bisector of angle A. If ∠B=72∘ and ∠C=26∘ then what is the measure of ∠DAE ?
त्रिभुज ABC में, AD, BC पर लम्ब है जो D पर डाला गया है तथा AE कोण A का द्विभाजक है | यदि ∠B=72∘ and ∠C=26∘ है, तो कोण DAE का मान ज्ञात करें |
View Solution
Knowledge Check
In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
 A10B30C60D15
A10B30C60D15In ΔPQR,∠Q>∠R PS is the bisector of ∠P and PT⊥PQ. If ∠SPT=28∘ and ∠R=23∘ then the measure of ∠Q is
A89∘B82∘C79∘D74∘In ΔPQR, If ∠R>∠Q, then
AQR>PRBPQ>PRCPQ<PRDQR>PR
In △ABC, if AB=AC and ∠BAC=40∘ ,then the measure of ∠B is
त्रिभुज ABC में, यदि AB=AC है तथा ∠BAC=40∘ है, तो कोण B का मान क्या होगा ?
View SolutionS is the incentre of △PQR. If ∠PSR=125∘ , then the measure of ∠PQR is:
S, त्रिभुज PQR का अंतःकेंद्र है | यदि ∠PSR=125∘ है, तो कोण PQR का मान ज्ञात करें |
View SolutionInternal bisectors of ∠Q and ∠R of traingle PQR intersect at O.If angle ROQ= 96 then the value of angle RPQ is
View SolutionIn ΔPQT,PQ=PT. The points R and S are on QT such that PR = PS. If ∠PTS=62∘and∠RPS=34∘, then measure of ∠QPR is
View SolutionIn ΔPQT,PQ=PT . The points R and S are on QT such that PR = PS . If ∠PTS=62∘and∠RPS=34∘ then measure of ∠QPR is
View Solution
