फलन x=Asin2ωt+Bcos2ωt+Csinωt×cosωt सरल आवर्ती गति प्रदर्शित करता है।
A , B ,और C के किसी भी मान के लिए ( C =0 छोड़कर)
यदि A = -B , C =2B , आयाम =∣∣B√2∣∣
यदि A=B,C=0
यदि A = B , C = 2B , आयाम =|B|
The correct Answer is:A, B, D
(abd ) (abd)x=A2(1−cos2ωt)+B2(1+cos2ωt)+C2sin2ωt
(a) A=0,B=0 के लिए
(x=C2sin2ωt)
(b) A=−B और C =2B के लिए,
x=Bcos2ωt+Bsin2ωt
परिमाण =∣∣B√2∣∣
(c)A=B,C=2B के लिए
x=B+Bsin2ωt
यह भी सरल आवर्त गति प्रदर्शित करता है।
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - JEE Section (Reasoning Type Questions)2videos
सरल आवर्त गति
- BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - JEE Section (Comprehension Type Questions)12videos
सरल आवर्त गति
- BOOK - ERRORLESS HINDICHAPTER - सरल आवर्त गति EXERCISE - Graphical Question (Objective Questions )14videos
सरल आवर्त गति
- BOOK - ERRORLESS HINDICHAPTER - विधुत चुम्बकीय प्रेरण EXERCISE - Self Evaluation Test विधुत चुम्बकीय प्रेरण17videos
विधुत चुम्बकीय प्रेरण
- BOOK - ERRORLESS HINDICHAPTER - स्थिर वैद्युतEXERCISE - Self Evaluation Test8videos
स्थिर वैद्युत
Similar Questions
यदि बल नियतांक क्रमशा k1 एवं k2 वाली दो कमानियां, S1 एवं S2 एक समान बल से तानित की जाए, तब यह पाया जाता है, की कमानी S1 पर कमानी S2 के मुकाबले अधिक कार्य किया जाता है।
कथन-I : यदि कमानियां एकसमान मात्रा से तनित की जाती है , तब S1 पर किया गया कार्य S2 पर किये गए कार्य से अधिक है
कथन-2 : k1<k209:00View Solutionजब m द्रव्यमान का एक कण :-अक्ष पर V(x) = kx2', स्थितिज ऊर्जा से गतिमान होता है, तब यह सरल आवर्त गति करता है। इसका आवर्तकाल √mk के समानुपाती होता है, जो कि विमीय विश्लेषण द्वारा आसानी से निकाला जा सकता है। हालाँकि, यदि किसी एक कण की स्थितिज ऊर्जा x = 0 के दोनों तरफ kx2 से । भिन्न तरह से बढ़े तथा कण की कुल ऊर्जा इतनी हो कि वह अनन्त तक पलायन न कर सके, तब भी कण की गति आवर्ती हो सकती है। m द्रव्यमान का एक कण x-अक्ष पर गति करता है जहाँ । x | के केन्द्र के पास होने पर स्थितिज ऊर्जा V(x) = ax4, (a>0) है तथा |x|>X0 के लिए स्थितिज ऊर्जा V(x) = V0, है (चित्र देखें) .
Q |x|> X0 के लिए कण का त्वरण-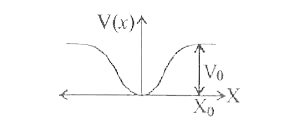
View Solutionएक कण स. आ. गति कर रहा है। इस कण के विस्थापन तथा त्वरण के बीच खींचे गए ग्राफ की प्रकृति होगी
04:10View Solutionचित्र में चार तार लूपो को दिखाया गया है। जिनकी भुजाओ की लम्बाई L या 2L है सभी चारो एकसमान वेग से एक समरूप चुम्बकीय क्षेत्र →B (कागज़ तल के लम्बवत बाहर की ओर) से गुजरते है। जब ये चुम्बकीय क्षेत्र से गुजरते है तब इनमे उत्पन्न वि. वा. बल. के परिमाण के आधार पर इसका क्रम क्या होगा
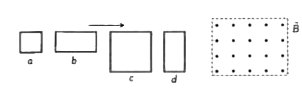
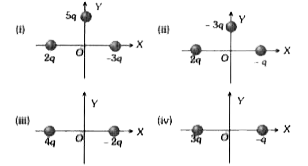
03:12View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
07:51View SolutionWhich of the following functions of time represent (a) simple harmonic (b) periodic but not simple harmonic and (c ) non periodic motion? Give period for each case of periodic motion (omega is nay positive constant) (1) Sin^(3) omegat (2) 3cos (pi//4 -2 omegat) (3) cos omegat +cos 3 omegat + cos 5 omegat (4) e^(-omega^(2)t^(2)) (5) 1 + omegat +omega^(2) t^(2)
01:45View SolutionFuncation x=Asin2ωt+Bcos2ωt+Csinωtcosωt Represents SHM.
04:12View SolutionA x and y co-ordinates of a particle are x=A sin (omega t) and y = A sin(omegat + pi//2) . Then, the motion of the particle is
04:13View SolutionFind the resulting amplitude A' and the phase of the vibrations delta S = Acos(omegat) + A/2 cos (omegat + pi/2) + A/2 cos (omega t + pi) + A/8 cos (omegat + (3pi)/(2)) = A' cos (omega t + delta)
12:39View Solutionनिचे दिए गये समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परन्तु सरल गति नहीं, तथा (c) अनावर्ती गति को निरूपण करते है। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए : (ω कोई धनात्मक अचर है।)
(a) sinωt−cosωt
(b) sin3ωt
(c) 3cos(π4−2ωt)
(d) cosω+cos3ωt+cos5ωt
(e) exp (−ω2t2)
(f) 1+ωt+ω2t204:40View SolutionIf dispolacement x at time t is x=acosωt−bsinωt, where ω is a constant, then: acceleration=
02:10View SolutionIf y=sin omegat-cos omega t then S.T. the function represents a SHM.
05:04View SolutionWhat is the time period for the function f(t) = sin omegat + cos omega t may represent the simple harmonic motion ?
04:11View SolutionWhich of the following functions of time represents (a) simple ideal speed and (b) periodic motion but not simple periodic motion? Find the period of each (a) sin omega t - cos omega t (b) sin ^(2) omegat.
06:35View Solutionनिम्न में से कौन से फलन सरल आवृति गति व्यक्त करते है।
(i) sin2ωt
(ii) sinωt+2cosωt
(iii) sinωt+cos2ωt08:41View SolutionIn the following functions showing the motion of a particle: (A) y= sin omegat -cos omegat (B) y= sin^(3) omega t (C ) y= 5 cos ""((3pi)/(4) -3 omegat ) (D) y= 1 +omegat +omega ^(2) t^(2) Who
05:20View Solution