माना कि S एक वृत्त है जो xy समतल में समीकरण x2+y2=4 के द्वारा परिभाषित है।
माना कि P वृत्त S पर स्थित एक ऐसा बिन्दु है जिसके दोनों निर्देशांक धनात्मक है। माना कि वृत्त S के बिन्दु P पर स्पर्शी निर्देशांक अक्षों को बिन्दुओं M और N पर प्रतिच्छेद करती है। तब रेखाखण्ड MN के मध्य बिन्दु से गुजरने वाले वक्र का समीकरण है
x+y=4
(x−4)2+(y−4)2=16
(x−4)(y−4)=4
xy=4
The correct Answer is:A
Step by step video, text & image solution for माना कि S एक वृत्त है जो xy समतल में समीकरण x^(2)+y^(2)=4 के द्वारा परिभाषित है। माना कि P वृत्त S पर स्थित एक ऐसा बिन्दु है जिसके दोनों निर्देशांक धनात्मक है। माना कि वृत्त S के बिन्दु P पर स्पर्शी निर्देशांक अक्षों को बिन्दुओं M और N पर प्रतिच्छेद करती है। तब रेखाखण्ड MN के मध्य बिन्दु से गुजरने वाले वक्र का समीकरण है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Matrix Match type questions)8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - Solved Multiple Choice Questions (वृत्त का समीकरण, वृत्त से सम्बंधित ज्यामितीय प्रश्न)122videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Reasoning type questions )8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)7videos
शांकव परिच्छेद
Similar Questions
कॉलम I में दिए गए वक्त्तव्यों का कॉलम II में दिए गए गुणधर्मों से सुमेल करें
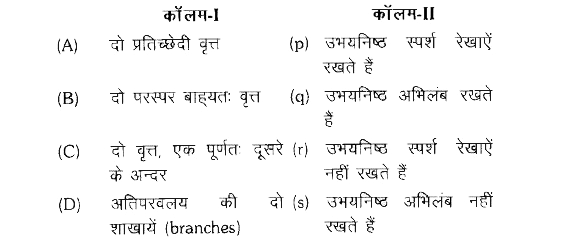
02:46View Solutionवृत्त x2+y2−2x+4y+3=0 के अंतर्गत एक वर्ग खींचा गया है जिसकी भुजायें निर्देशांक अक्षों के समान्तर है। तब बर्ग का एक शीर्ष है
02:13View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।04:05View Solution
03:18View Solution
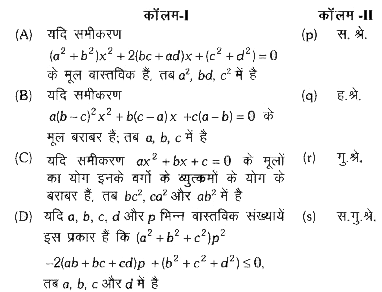
03:41View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
02:21View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
05:05View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
08:00View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
04:24View Solutionमाना PQ और RS,r त्रिज्या के वृत्त के व्यास के सिरों पर खींची गई स्पर्शियाँ है। यदि PS और RQ परिधि पर स्थिति बिन्दु X पर प्रतिच्छेद करते है तो 2r बराबर है-
04:26View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
05:40View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
02:34View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
06:39View Solutionयदि वृत्त x2+y2=1 की एक स्पर्श रेखा निर्देशांक अक्षो को भिन्न बिन्दुओ P और Q पर प्रतिच्छेद करती है, तो PQ के मध्य -बिंदु का बिन्दुपथ (locus) है
02:57View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
05:40View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
03:18View Solution