माना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है।
कथन -1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
The correct Answer is:C
Step by step video, text & image solution for माना L_(1)=2x+3y+p-3=0, L_(2):2x+3y+p+3=0 जहाँ p एक वास्तविक संख्या है तथा C=x^(2)+y^(2)+6x-10y+30=0 कथन-1 : यदि रेखा L_(1) वृत्त C की जीवा है, तब रेखा L_(2) सदैव वृत्त C का व्यास नही होगी तथा कथन-2 : यदि रेखा L_(1) वृत्त C का व्यास है, तब रेखा L_(2) वृत्त C की जीवा नहीं होगी। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Comprehension type questions)
46 Videos
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Matrix Match type questions)
8 Videos
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (More than one correct answers)
28 Videos
- वर्ग समीकरण एवं असमिकायें BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)
2 Videos
- शांकव परिच्छेद BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)
7 Videos
Similar Questions
समबाहु त्रिभुज PQR के अंतनिर्हित एक वृत C स्थित है जिसकी त्रिज्या 1 है। त्रिभुज की भुजाओ PQ, QR, RF को बिंदु D, E, F पर स्पर्श करता है। रेखा PQ का समीकरण √3x+y−6=0 तथा बिंदु D(3√32,32) है। यह भी दिया है की मूलबिंदु व C का केंद्र रेखा PQ के एक तरफ ही स्थित है।
वृत C का समीकरण है
View Solutionकॉलम I में दिए गए वक्त्तव्यों का कॉलम II में दिए गए गुणधर्मों से सुमेल करें
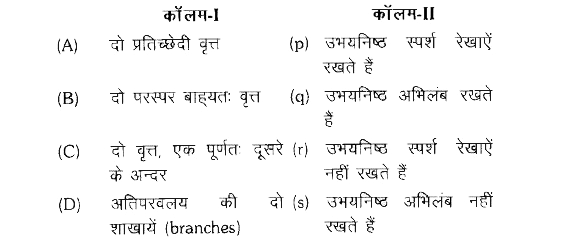
View Solutionमाना कि L1 मूलबिन्दु से गुजरने वाली एक सरल रेखा है तथा सरल रेखा L2 का समीकरण x+y=1 है। यदि वृत्त x2+y2−x+3y=0 द्वारा L1 और L2 पर काटे गये अन्तःखण्ड बराबर हैं, तो निम्नलिखित में से कौन-सा समीकरण रेखा L1 को निरूपित करता है
View Solution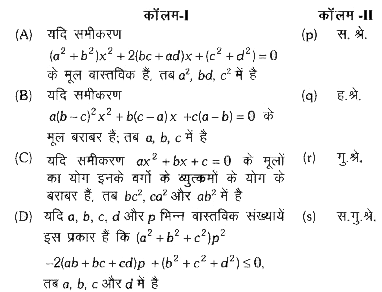
View Solution
View SolutionConsider, L_(1) : 2x + 3y + p – 3 = 0 , L_(2) : 2x + 3y + p + 3 = 0 , where p is a real number, and C : x^(2)+y^(2)+6x–10y+30=0 Statement-I : If line L_(1) is a chord of circle C, then line L_(2) is not always a diameter of circle C. and Statement-II : If line L_(1) is a diameter of circle C, then line L_(2) is not a chord of circle C.
View Solutionदी गई आकृति में O वृत्त का केंद्र तथा SCT बिंदु C पर स्पर्श रेखा है। यदि ∠ACS=57∘ हो ,तो ∠OAC की माप है -
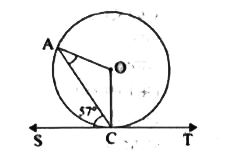
View Solutionरेखायें l1 व l2 प्रतिच्छेदी है तो उनके बीच की न्यूनतम दूरी होगी -
View SolutionConsider the lines given by
L1:x+3y−5=0, L2:3x−ky−1=0 L3:5x+2y−12=0
Column-IColumn-II(A),L1,L2,L3 are concurrent, if(p)k=−9(B) One of L1,L2,L3 is parallel to at least one of the other two, if(q)k=−65(C)L1,L2,L3 from a triangle, if(r)k=56(D)L1,L2,L3 do not from a triangle, if(s)k=5
View Solutionवृत्त की छेदन रेखा PQ है। छेदन रेखा PQ के स्पर्श रेखा बनने का प्रतिबन्ध किखिये।
View Solutionवृत्त की छेदन रेखा PQ है। छेदन रेखा PQ के स्पर्श रेखा बनने का प्रतिबन्ध किखिये।
View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।
View Solutionमाना बिंदु (h,k), (1,2) तथा (−3,4) एक रेखा L1 पर स्थित है। यदि बिन्दुओ (h,k) तथा (4,3) से होकर जाने वाली रेखा L2 रेखा L1 के लंबवत है, तो kh बराबर है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionउन बिन्दुओं को मिलाने वाली जीवा की लम्बाई, जिन पर सरल रेखा x3+y4=1 , वृत्त x2+y2=16925 को काटती है, है
View Solution
