वृत्तों के एक निकाय में, प्रत्येक दो वृत्त जिनके मूलाक्ष समान हो समाक्ष कहे जाते है।
समाक्ष वृत्त निकाय का व्यापक समीकरण है। जहाँ g भिन्न-भिन्न वृत्त निकाय के लिए भिन्नात्मक है तथा c सभी वृत्तों के लिए समान है, उभयनिष्ठ मूलाक्ष y-अक्ष तथा केन्द्रों की रेखा x-अक्ष है।
मूलाक्ष के दिए गये समीकरण तथा निकाय S=0 के एक वृत्त को रखने वाले समाक्ष वृत्त निकाय का समीकरण है। दिए गये निकाय के दो वृत्तों के समीकरणों
को रखने वाले समाक्ष वृत्त निकाय का समीकरण है।।
समाक्ष वृत्त निकाय के सदस्यों जो शून्य त्रिज्या के हैं निकाय के सीमान्त बिन्दु कहे जाते हैं।
यदि A,B,C तथा तीन समाक्ष वृत्तों के क्रमशः केन्द्रक तथा त्रिज्याएँ हो, तो
BC.CA.AB
2BC.CA.AB
इनमें से कोई नहीं
The correct Answer is:B
Topper's Solved these Questions
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Matrix Match type questions)
8 Videos
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - Solved Multiple Choice Questions (वृत्त का समीकरण, वृत्त से सम्बंधित ज्यामितीय प्रश्न)
122 Videos
- वृत्त तथा वृत्तों का निकाय BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Reasoning type questions )
8 Videos
- वर्ग समीकरण एवं असमिकायें BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)
2 Videos
- शांकव परिच्छेद BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)
7 Videos
Similar Questions
कॉलम I में दिए गए वक्त्तव्यों का कॉलम II में दिए गए गुणधर्मों से सुमेल करें
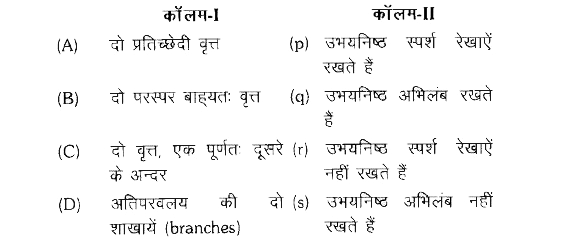
View Solutionवृत्त x2+y2−2x+4y+3=0 के अंतर्गत एक वर्ग खींचा गया है जिसकी भुजायें निर्देशांक अक्षों के समान्तर है। तब बर्ग का एक शीर्ष है
View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।
View Solution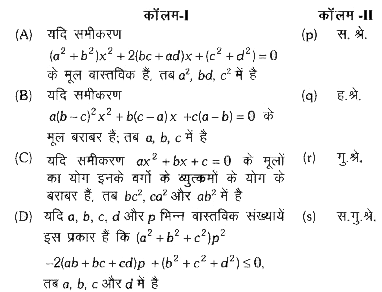
View Solution
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionk के सभी मानो के लिए वृत्त x2+y2−kx−2ky+k2=0 स्पर्श करता है -
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View SolutionY - अक्ष के समीकरण का सममित रूप …………. है।
View Solutionλ के किस मान के लिए निम्न समीकरण के निकाय
2x−y−2z=2,x−2y+z=−4,x+y+λz=4 का कोई हल नहीं है
View Solutionयदि निकाय के समीकरणों x−ky−z=0,kx−y−z=0 तथा x+y−z=0 का एक अशून्य हल है, तो k का संभावित मान होगा
View Solutionयदि समीकरण निकाय x+ay=0,ax+y=0 और ax+z=0 के अनंत हल है, तब a का मान है
View Solutionc∈R का अधिकतम मान, जिसके लिए रेखिक समीकरण निकाय x−cy−cz=0,cx−y+cz=0,cx+cy−z=0 का एक अत्युच्च हल है, है
View Solution
