माना कि S एक वृत्त है जो xy समतल में समीकरण के द्वारा परिभाषित है।
माना कि और वृत्त S की ऐसी जीवाएं हैं जो बिन्दु से गुजरती हैं और क्रमश: x-अक्ष व y-अक्ष के समान्तर हैं। माना कि की वह जीवा है जो से गुजरती है और जिसकी प्रवणता -1 है। माना कि और पर S की स्पर्शियां पर मिलती हैं, और पर S की स्पर्शियां पर मिलती हैं, तथा और पर S की स्पर्शियां पर मिलती हैं। तब बिन्दु और से गुजरने वाले वक्र का समीकरण है
The correct Answer is:A
Step by step video, text & image solution for माना कि S एक वृत्त है जो xy समतल में समीकरण x^(2)+y^(2)=4 के द्वारा परिभाषित है। माना कि E_(1)E_(2) और F_(1)F_(2) वृत्त S की ऐसी जीवाएं हैं जो बिन्दु P_(0)(1, 1) से गुजरती हैं और क्रमश: x-अक्ष व y-अक्ष के समान्तर हैं। माना कि G_(1)G_(2), S की वह जीवा है जो P_(0) से गुजरती है और जिसकी प्रवणता -1 है। माना कि E_(1) और E_(2) पर S की स्पर्शियां E_(3) पर मिलती हैं, F_(1) और F_(2) पर S की स्पर्शियां F_(3) पर मिलती हैं, तथा G_(1) और G_(2) पर S की स्पर्शियां G_(3) पर मिलती हैं। तब बिन्दु E_(3),F_(3) और G_(3) से गुजरने वाले वक्र का समीकरण है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Matrix Match type questions)8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - Solved Multiple Choice Questions (वृत्त का समीकरण, वृत्त से सम्बंधित ज्यामितीय प्रश्न)122videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वृत्त तथा वृत्तों का निकाय EXERCISE - JEE Advanced (Reasoning type questions )8videos
वृत्त तथा वृत्तों का निकाय
- BOOK - ERRORLESS HINDICHAPTER - वर्ग समीकरण एवं असमिकायें EXERCISE - JEE Advanced (Matrix Match type questions)2videos
वर्ग समीकरण एवं असमिकायें
- BOOK - ERRORLESS HINDICHAPTER - शांकव परिच्छेद EXERCISE - JEE Advanced (Matrix Match type questions)7videos
शांकव परिच्छेद
Similar Questions
कॉलम I में दिए गए वक्त्तव्यों का कॉलम II में दिए गए गुणधर्मों से सुमेल करें
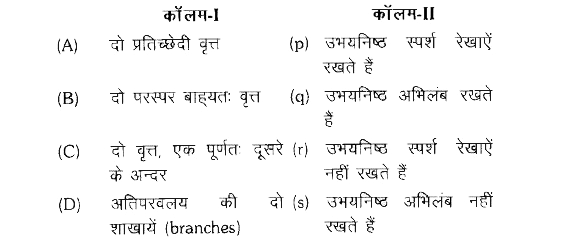
02:59View Solutionवृत्त x2+y2−2x+4y+3=0 के अंतर्गत एक वर्ग खींचा गया है जिसकी भुजायें निर्देशांक अक्षों के समान्तर है। तब बर्ग का एक शीर्ष है
05:19View Solutionमाना L1=2x+3y+p−3=0,L2:2x+3y+p+3=0
जहाँ p एक वास्तविक संख्या है तथा C=x2+y2+6x−10y+30=0
कथन-1 : यदि रेखा L1 वृत्त C की जीवा है, तब रेखा L2 सदैव वृत्त C का व्यास नही होगी तथा
कथन-2 : यदि रेखा L1 वृत्त C का व्यास है, तब रेखा L2 वृत्त C की जीवा नहीं होगी।03:08View Solution
02:13View Solution
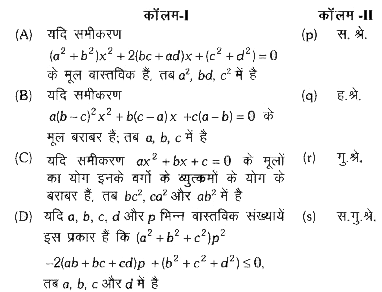
02:12View Solutionमाना कि X={1,2,3,4,5,6,7,8,9}, माना कि X में सम्बन्ध R1 तथा R2 इस प्रकार हैं कि R1={(x,y):x−y,3 से विभाज्य हैं,x≠y} तथा R2={(x,y):{x,y}⊂{1,4,7} या {x,y}⊂{2,5,8} या {x,y}⊂{3,6,9} जहाँ ⊂ का अर्थ उपसमुच्चय से हैं| दिखाएं कि R1=R2
08:08View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
06:12View Solutionमाना a,b,c वास्तविक संख्याएं है। माना x,y,z ऐसी वास्तविक संख्या है जो कभी शून्य नहीं हैं तथा x=cy+bz,y=az+cx तथा z=bx+ay, तो a2+b2+c2+2abc का मान है:
05:05View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
04:26View Solutionबेज प्रमेय के अनुसारE1,E2 प्रतिदर्श समष्टि के विभाजन का निर्माण करती है अर्थात E1,E2 असंयुक्त है और E1∩E2=S ,A एक शून्येतर प्रायिकता कि घटना है , तब P(E1A)=.......... और P(E2A)=..........
02:27View Solutionमाना z1=10+6i और z2=4+6i यदि सम्मिश्र संख्या z इस प्रकार है कि (z−z1)(z−z2) का कोणांक π4 है, तो सिद्ध कीजिए कि |z−7−9i|=3√2.
02:32View Solutionमाना ω एक सम्मिश्र संख्या ऐसी है कि 2ω+1=z जहाँ, z=√−3 है। यदि ∣∣ ∣ ∣∣1111−ω2−1ω21ω2ω2∣∣ ∣ ∣∣=3k है तो k बराबर है
02:36View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
02:42View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
03:16View Solutionदिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. वास्तविक संख्या S, निम्न अन्तराल में है03:22View Solutionउस सरल रेखा का समीकरण जो बिन्दु (1,-2) से गुजरती है तथा रेखा 3x-5y+7=0 के लम्बवत है, है
04:08View Solution