h ऊँचाई की मीनार के पाद से 2h दूरी पर स्थित एक बिन्दु पर मीनार तथा उसके शिखर पर स्थित एक डण्डा समान कोण अन्तरित करते है। तब डण्डे की ऊँचाई होनी चाहिये।
5h/3
4h/3
7h/3
3h/2
The correct Answer is:A
Step by step video, text & image solution for h ऊँचाई की मीनार के पाद से 2h दूरी पर स्थित एक बिन्दु पर मीनार तथा उसके शिखर पर स्थित एक डण्डा समान कोण अन्तरित करते है। तब डण्डे की ऊँचाई होनी चाहिये। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Exercise134videos
त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - JEE Advanced47videos
त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Solved Multiple Choice Question (त्रिभुजों से सम्बध्द वृत्त )10videos
त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- BOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )3videos
गणितीय तर्कशास्त्र
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)5videos
त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकाये
Similar Questions
यदिsin2θ=cosθ,0<θ<π तो θ के संभव मान है।
00:59View Solution0<θ<π2 के लिए 6Σm=1cosec(θ+(m−1)π4)cosec(θ+mπ4)=4√2 का के हल निम्न है।
05:05View Solutionएक त्रिभुज में यदि r1=2r2=3r3 तब ab+bc+ca बराबर है।
04:29View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।45:19View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
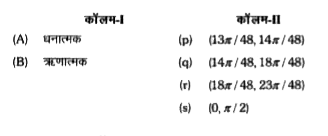 42:52View Solution
42:52View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
36:35View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
36:36View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
02:14View Solutionऊँचाई तथा दूरी पर प्रश्न (Part-3)
03:32View Solutionसरल रेखाएँ|एक बिन्दु की रेखा से दूरी#!#दो समांतर रेखाओ के बीच की दूरी#!#प्रश्नो पर चर्चा
05:15View SolutionRevision|ऊँचाई तथा दूरी पर प्रश्न
01:38View SolutionRevision |ऊँचाई तथा दूरी पर प्रश्न
49:45View SolutionA tower stands on the top of a building which is 40 metres high. The angle of depressiotf of a point situated on the ground-from the top and bottom of the tower are found to Be 60∘ and 45∘ respectively.What is the height (in metres) of tower?
एक भवन जिसकी ऊँचाई 40 मीटर है, के शिखर पर एक मीनार खड़ी है। मीनार के शिखर तथा पांद बिन्दु से भूमि पर स्थित एक बिन्दु का अर्वनमन कोण क्रमशः 60∘ तथा 45∘ है। मीनार की ऊँचाई (मीटर में) क्या है ?01:39View SolutionHeight of a tower is 120 metres. The angle of elevation of the top of tower from a point B is 75^@ .Point B is on the ground level. What is the distance (in metres)of point B from the base of tower? एक भीनार की ऊँचाई 120 मीटर है। बिंदु B से मीनार की चोटी का उन्नयन कोण 75^@ है। बिंदु B जमीन की सतह पर है। मीनार के आधार से बिंदु B की दूरी (मीटर में) क्या है?
02:33View SolutionA vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angle of elevation of the bottom of the flag staff is alpha and that of the top of the flag staff is beta . then the height of the tower is एक ऊर्ध्वाधर मीनार एक क्षेतिज समतल पर खड़ी है और उसके ऊपर 1 ऊँचाई का ऊर्ध्वाधर ध्वजखण्ड लगा है। समतल पर एक बिन्दु पर ध्वजदण्ड के तल का उन्नयन कोण alpha है और ध्वजदण्ड के शीर्ष भाग का beta है। मीनार की ऊँचाई बताइए ?
View SolutionThe angle of elevation of a tower from a distance 50m from its foot is 30^@ . The height of the tower is- एक मीनार का उसके मूल आधार (पाद) से 50 मीटर दूरी से उन्नयन कोण 30^@ है। तदनुसार उस मीनार की ऊँचाई कितनी होगी?
39:47View Solution
