यदि tanα तथाtanβ समीकरण x2+px+q=0 के मूल है जबकि p≠0,q≠1 तब
sin2(α+β)+psin(α+β)cos(α+β)+qcos2(α+β)=q
tan(α+β)=pq−1
cos(α−β)=1−q
sin(α+β)=−p
The correct Answer is:A, B, C, D
Step by step video, text & image solution for यदि tan alpha तथाtan beta समीकरण x^(2) +px + q=0 के मूल है जबकि p ne 0 ,q ne 1 तब by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Exercise
134 Videos
- गणितीय तर्कशास्त्रBOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
Similar Questions
यदिsin2θ=cosθ,0<θ<π तो θ के संभव मान है।
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
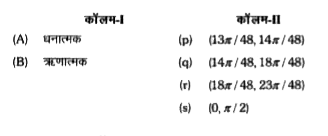
View SolutionIf tan alpha tan beta are the roots of the equation x^(2)+px+q=0(p!=0) then
View SolutionIf tanα,tanβ are the roots of the equation x2+px+q=0(p≠0) then
View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionयदि समीकरण x2+px+q=0 के मूल, α,β है और समीकरण x2−rx+s=0 के मूल α4,β4 है, तो समीकरण x2−4qx+2q2−r=0 के सदैव
View Solutionमाना a,b,c वास्तविक संख्याएं है, a≠0 यदि समीकरण a2x2+bx+c=0 का मूल α है तथा समीकरण a2x2−bx−c=0 का मूल β है तथा 0<α<β तो समीकरण a2x2+2bx+2c=0 का एक मूल γ किस प्रतिबन्ध को संतुष्ट करेगा?
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionमाना p,q∈R, यदि 2−√3 द्विघाती समीकरण x2+px+q=0 का एक मूल है, तो
View Solutionयदि समीकरण के Ax2+Bx+C=0 मूल α,β एव समीकरण x2+px+q=0 के α2,β2 हो तो p का मान है।
View Solutionयदि समीकरण के Ax2+Bx+C=0 मूल α,β एव समीकरण x2+px+q=0 के α2,β2 हो तो p का मान है।
View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
View Solutionयदि α,β द्विघात समीकरण x2+px+p3=0(p≠0) के मूल हो तथा (α,β) परवलय y2=x पर स्थित एक बिंदु हो, तो समीकरण के मूल होगा
View Solutionयदि tanα व् tanβ समीकरण x2−px+q=0 के मूल हो, तो sin2(α+β) का मान है
View Solution
