यदि b>1,sint>0,cost>0 तथा logb(sint)=x तब logb(cost) बराबर है।
12logb(1−b2x)
2log(1−bx/2)
logb√1−b2x
√1−x2
The correct Answer is:A, C
Step by step video, text & image solution for यदि b gt 1 , sin t gt 0 ,cos t gt 0 तथा log_(b ) (sin t ) =x तब log_(b ) (cos t ) बराबर है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Exercise
134 Videos
- गणितीय तर्कशास्त्रBOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
Similar Questions
यदिsin2θ=cosθ,0<θ<π तो θ के संभव मान है।
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
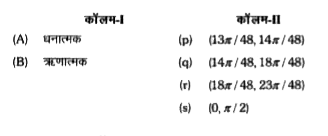
View SolutionIf b>1,sin t>0,cos t>0 and log_(b)(sin t)=x then log_(b)(cos t)=
View Solutionx=a cos t, y=b sin t
View SolutionLocus of centroid of the triangle whose vertices are (a cos t, a sin t), (b sin t, - b cos t) and (1, 0), where is a
View SolutionLocus of centroid of the triangle whose vertices are (acost,asint),(bsint−bcost)and(1,0) where t is a parameter, is
View Solutionकिसी त्रिभुज के केन्द्रक का बिन्दुपथ जिसके शीर्ष (acost,asint),(bsint,−bcost) और (1,0) (जहाँ t एक प्राचल है) है:
View SolutionThe maximum distance from the origin of a point on the curve x=asint−bsin(atb),y=acost−bcos(atb) , both a,b>0 , is-
View SolutionLet a>1 and b>1. If f(t) is a periodic function of period T and ∫∞0a−bif(t)dt=k∫T0a−btf(t)dt then k =
View SolutionLocus of centroid of the triangle whose vertices are (acost,asint),(bsint,−bcost) and (1, 0), where t is a parameter, is :
View SolutionLocus of centroid of the triangle whose vertices are (a cos t, a sin t),(b sin t , - b cos 1) and (1, 0), where 't' is a parameter, is :
View SolutionIf a>0,b>0,c>0 are in G.P. , then :
logax,logbx,logcx are in :
View SolutionIf a > 0, c >0, b =√ac and ac ≠1, N>0 , then logaN−logbNlogbN−logcN =
View SolutionThe length of the tangent to the curve x=asin3t,y=acos3t(a>0) at an arbitrary is
View Solution
