Question

पृथ्वी को एकसमान घनत्व का R त्रिज्या का गोला मान लें तथा इसके व्यासत: एक सुरंग की कल्पना करें। इस सुरंग में यदि किसी पिंड को पृथ्वी की सतह से विराम से गिराया जाए, तो सिद्ध करें कि पिंड सरल आवर्त गति निष्पन्न करेगा। इस गति का आवर्तकाल भी ज्ञात करें।

Explanation

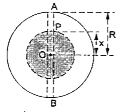
मान लिया पृथ्वी में व्यासतः खोदी गई सुरंग AOB में सतह A से m द्रव्यमान का एक पिंड विराम से मुक्त किया गया है। गुरुत्वाकर्षण के कारण यह केंद्र 0 की ओर गतिशील होगा और इसकी चाल ) पर महत्तम होगी। फिर, 0 से B की ओर जाने के क्रम में इसकी चाल घडते हुए B पर शून्य हो जाएगी और गुरुत्वाकर्षण के कारण ही पिंड उसी पथ पर अपनी गति को दुहराते हुए A पर पहुँचेगी और गति की पुनरावृत्ति होती रहेगी। अब गति पथ के किसी बिंदु P पर पिंड पर लगनेवाला आकर्षण बल
`F=Gxxmxx` त्रिज्या OP के गोले का द्रव्यमान/`OP^(2)`
`=(Gm(4)/(3)pi x^(3) rho)/(x^(2)) " " ` [ यहाँ `rho =` पृथ्वी का घनत्व `(M)/((4)/(3)pi R^(3)), OP=x` तथा M = पृथ्वी का द्रव्यमान]
`=Gm((4)/(3)pix^(3))/(x^(2))*(M)/((4)/(3)pi R^(3))=Gm*(M)/(R^(3))x`
चूँकि बल F तथा केंद्र 0 के सापेक्ष विस्थापन x परस्पर विपरीत दिशाओं में हैं, अतः `F=(GMm)/(R^(3))x`
या `ma=-(GM)/(R^(3))mx " " [ :. F=ma]`
या त्वरण `a=-(GM)/(R^(3))x " "....(1)`
समीकरण (1) से, त्वरण `prop` -विस्थापन, चूँकि G, M तथा R नियत राशियाँ हैं। अतः, पिंड की गति सरल आवर्त गति होगी, जिसके लिए `a=- omega^(2)x " "....(2)`
समीकरण (1) तथा (2) से `omega= sqrt((GM)/(R^(3)))`
या `(2pi)/(T)=sqrt((GM)/(R^(3)))` जहाँ पिंड का आवर्तकाल है
या `T = 2pi sqrt((R^(3))/(GM))` परंतु, `GM=gR^(2)`
`T=2pi sqrt((R^(3))/(gR^(2)))`
अतः, `T = 2pi qrt((R)/(g))`. यही अभीष्ट आवर्तकाल है।