आकाश (space) में किसी स्वेच्छ गति (arbitrary motion) के लिए निम्नांकित संबंधो में से कौन- कौन सही है ?
→aav=→v(t2)−→v(t1)t2−t1
[उपर्युक्त संबंधो में av (अर्थात average, या माध्य ) का अर्थ है वेग (→v) अथवा त्वरण (→a) का माध्य - मान समयांतराल (t2−t1) के बीच]
सही है, क्योकि परिभाषा के माध्य त्वरण = वेग परिवर्तन समयांतराल =Δ→vΔt=(→v−→u)Δt=→v(t2)−→v(t2)t2−t1
केवल (b) तथा (e) सही विकल्प है।
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.4 गति के नियम : घर्षण
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.5 कार्य , शक्ति और ऊर्जा
33 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.2 अदिश एवं सदिश
40 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
50 g द्रव्यमान का एक पत्थर ऊर्ध्वाधरतः ऊपर की ओर फेंका गया है। निम्नांकित परिस्थितियों के लिए पत्थर पर लग रहे नेट बल का परिमाण एवं दिशा बताए।
(a)ऊपर की ओर गति के क्रम में
(b) नीचे की ओर गति के क्रम में
(c) गति के उच्चतम बिंदु पर जहाँ पत्थर क्षणिक विराम (momentary rest) में रहता है
(d) विराम में स्थित रेलगाड़ी की खिड़की से पत्थर को गिराने के तुरंत बाद
View Solutionकिसी वस्तु पर आरोपित बल द्वारा किया गया कार्य धनात्मक अथवा ऋणात्मक दोनों हो सकता है नीचे दिए गए प्रकथनो को ध्यानपूर्वक पढ़कर करणसहित बताएँ कि निम्नांकित कार्य धनात्मक है अथवा ऋणात्मक ?
रस्से से बंधी किसी बाल्टी को रस्सी द्वारा कुएँ से बाहर निकलने में किसी व्यक्ति द्वारा किया गया कार्य
View Solutionयदि →a=3ˆi+4ˆj तथा →b=7ˆi+24ˆj तो वह सदिश ज्ञात करे जिसका परिमाण →b के तुल्य हो तथा दिशा →aके समांतर हो।
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
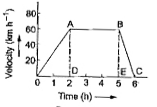
View SolutionTwo particles of masses m_(1) and m_(2) in projectile motion have velocities vec(v)_(1) and vec(v)_(2) , respectively , at time t = 0 . They collide at time t_(0) . Their velocities become vec(v')_(1) and vec(v')_(2) at time 2 t_(0) while still moving in air. The value of |(m_(1) vec(v')_(1) + m_(2) vec(v')_(2)) - (m_(1) vec(v)_(1) + m_(2) vec(v)_(2))|
View SolutionThe quantity ∫t2t1→Vdt represents:
View SolutionLet→V=vxˆi+vyˆj+vzˆk, then ∫t2t1Vy represents: (for the duration t1→t2)
View SolutionFor any arbitrary motion in space, which of the following relations are true?
(a) vaverage=(1/2)(v(t1)+v(t2))
(b) vaverage=[r(t2)−r(t1]/(t2−t1)
(c) v(t)=v(0)+at
(d) aaverage=[v(t2)−v(t1)]/(t2−t1)
The average stands for average of the quantity over time interval t1 to t2
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionकिसी द्विकस्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंधो में से कौन - सा सत्य है ?
→v औसत =[→r(t2)−→r(t1)]/(t2−t1)
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) Vaverage=(1/2)(v(t1)+v(t2))
(b) Vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) V(t)=V(0)+at
(d) r(t)=r(0)+v(0)T+(1/2)at2
(e ) aaverage=[v(t2)−v(t1)]/(t2−t1)
(The average stands for average of the quantity over the time interval t1 to t2)
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) V_("average")=(1//2)(v(t_(1))+v(t_(2))) (b) V_("average")=[r(t_(2))-r(t_(1))]//(t_(2)-t_(1)) (c ) V(t)=V(0)+at (d) r(t) =r(0)+v(0)T+(1//2)at^(2) (e ) a_("average")=[v(t_(2))-v(t_(1))]//(t_(2)-t_(1)) (The average stands for average of the quantity over the time interval t_(1)" to "t_(2))
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) Vaverage=(1/2)(v(t1)+v(t2))
(b) Vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) V(t)=V(0)+at
(d) r(t)=r(0)+v(0)T+(1/2)at2
(e ) aaverage=[v(t2)−v(t1)]/(t2−t1)
(The average stands for average of the quantity over the time interval t1 to t2)
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) Vaverage=(1/2)(v(t1)+v(t2))
(b) Vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) V(t)=V(0)+at
(d) r(t)=r(0)+v(0)T+(1/2)at2
(e ) aaverage=[v(t2)−v(t1)]/(t2−t1)
(The average stands for average of the quantity over the time interval t1 to t2)
View SolutionFollowing are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S). a) V_(av)=(1)/(2)[v(t_(1))+v(t_(2))] b) V_(av)=(r(t_(2))-r(t_(2)))/(t_(2)-t_(1)) c)r= (1)/(2)(v(t_(2))-v(t_(1))(t_(2)-t_(1)) d) a_(av)=(v(t_(2))-v(t_(1)))/(t_(2)-t_(1))
View SolutionFollowing are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S).
a) Vav=12[v(t1)+v(t2)]
b)Vav=r(t2)−r(t2)t2−t1
c)r=12(v(t2)−v(t1)(t2−t1)
d)aav=v(t2)−v(t1)t2−t1
View Solution
