Following are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S).
a) Vav=12[v(t1)+v(t2)]
b)Vav=r(t2)−r(t2)t2−t1
c)r=12(v(t2)−v(t1)(t2−t1)
d)aav=v(t2)−v(t1)t2−t1Solution in Telugu
a and b
a and d
b and c
a and c
The correct Answer is:D
Step by step video, text & image solution for Following are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S). a) V_(av)=(1)/(2)[v(t_(1))+v(t_(2))] b)V_(av)=(r(t_(2))-r(t_(2)))/(t_(2)-t_(1)) c)r=(1)/(2)(v(t_(2))-v(t_(1))(t_(2)-t_(1)) d)a_(av)=(v(t_(2))-v(t_(1)))/(t_(2)-t_(1)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise 2A
30 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise -2
76 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems Based On Calculus
28 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise
84 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
Similar Questions
(A): Displacement of a body may be zero when distance travelled by it is not zero.
(R) : The displacement is the longest distance between initial and final positions..
View SolutionA person travels along a straight road for half the distance with velocity V1 and the remaining half distance with velocity V2 the average velocity is given by
View SolutionThe motion of a particle along a straight line is described by the function s=6+4t2−t4
in SI units.Find the velocity ,acceleration ,at t=2s,and the average velocity during 3rd second.
View SolutionA person runs along a circular path of radius 5m. Find the magnitude of the displacement if he runs all the way around the circle ?
View SolutionThe system shown in the figure is given an acceleration 'a' towards left. Assume all contact surfaces to be smooth (m: mass of the sphere) The magnitude of the contact force between wedge and sphere between wedge and sphere at A is xmg√3 then 'x' is

View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.:

(a) Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2:
(a) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) v(t2)=v(t1)+a(t2−t1)
(c) vaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(v(t2)−v(t1))/(t2−t1)
(e) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(f) x(t2)−x(t1) = area under the v−t curve bounded by the t-axis and the dotted line shown.
View SolutionFor any arbitrary motion in space, which of the following relations are true?
(a) vaverage=(1/2)(v(t1)+v(t2))
(b) vaverage=[r(t2)−r(t1]/(t2−t1)
(c) v(t)=v(0)+at
(d) aaverage=[v(t2)−v(t1)]/(t2−t1)
The average stands for average of the quantity over time interval t1 to t2
View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र 3.29 में दिखाया गया है :

नीचे दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-सा सूत्र सही है :
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t-अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |
View Solutionकिसी दीकस्थान पर एक स्वेच्छ गति के लिए निम्नलिखित सम्बन्धो में से कौन-सा सत्य है ?
(a) vऔसत=(1/2)[v(t1)+v(t2)]
(b) vऔसत=[r(t2)−r(t1)]/(t2−t1)
(c ) v(t)=v(0)+at
(d) r(t)=r(0)+v(0)t+(1/2)at2
(e ) aऔसत=pv(t2)−v(t1)]/(t2−t1)
यहाँ 'औसत' का आशय समय अन्तराल t2 व t1 से सम्बन्धित भौतिक राशि के औसत मान से है |
View Solutionयदि वस्तु समय t1 तक वेग v1 से तथा समय t2 तक वेग v2 से चले तो उसका औसत वेग होगा :
vav=v1t1+v2t2t1+t2
View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र में दिखाया गया है -
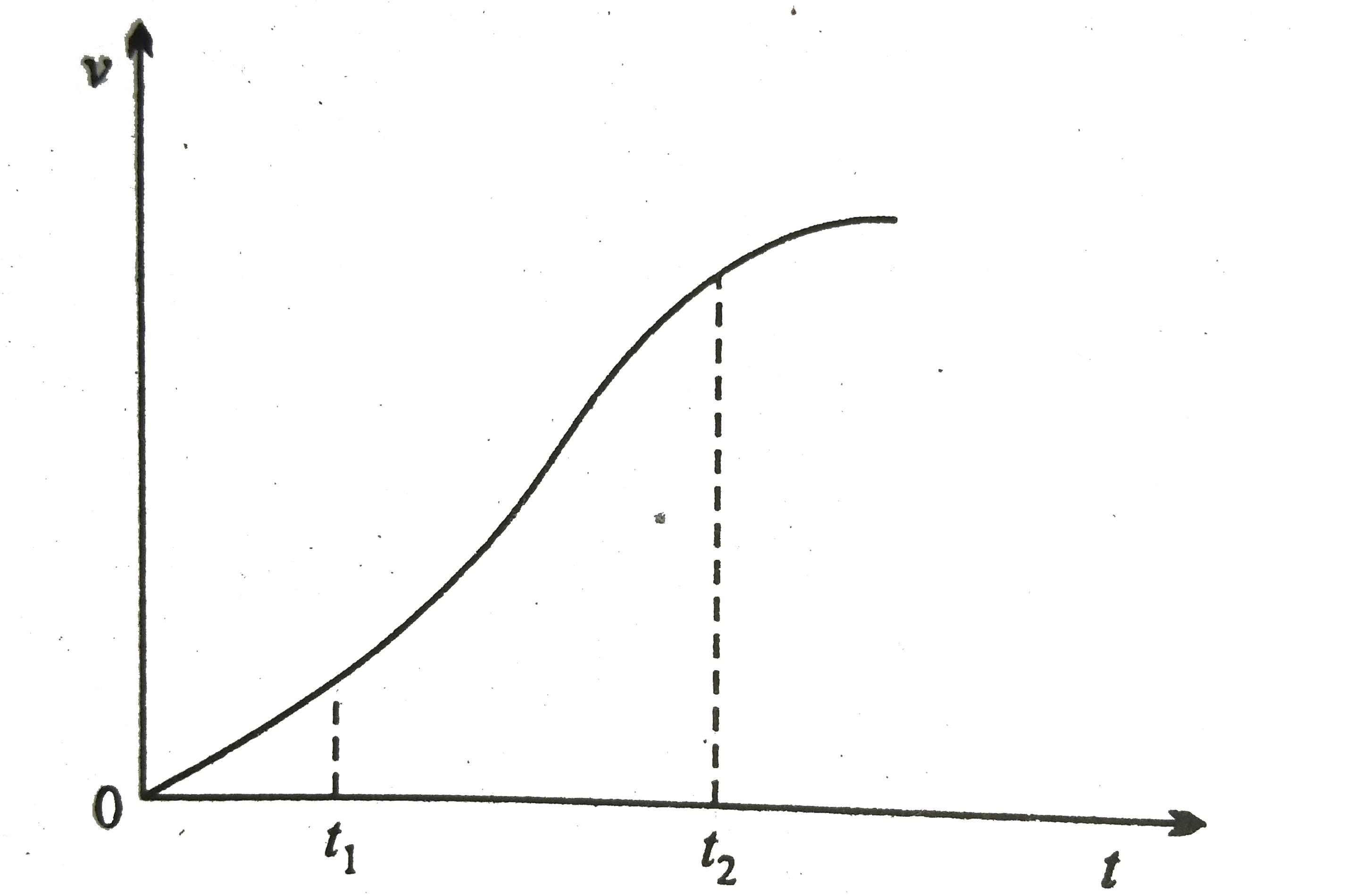
नीचे दिये सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं -
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) vaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t− अक्ष तथा दिखाई गाड़ी बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल ।
View Solutionएकविमीय गति में किसी कण का वेग - समय ग्राफ चित्र में दिखाया गया है-
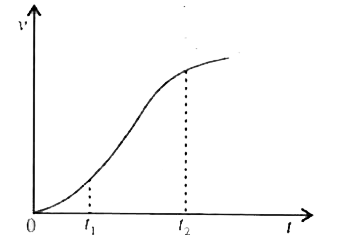
दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन - से सूत्र सही हैं
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(i8i) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t− अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) Vaverage=(1/2)(v(t1)+v(t2))
(b) Vaverage=[r(t2)−r(t1)]/(t2−t1)
(c ) V(t)=V(0)+at
(d) r(t)=r(0)+v(0)T+(1/2)at2
(e ) aaverage=[v(t2)−v(t1)]/(t2−t1)
(The average stands for average of the quantity over the time interval t1 to t2)
View SolutionFor any arbitrary motion in space , which of the following relations are true : (a) V_("average")=(1//2)(v(t_(1))+v(t_(2))) (b) V_("average")=[r(t_(2))-r(t_(1))]//(t_(2)-t_(1)) (c ) V(t)=V(0)+at (d) r(t) =r(0)+v(0)T+(1//2)at^(2) (e ) a_("average")=[v(t_(2))-v(t_(1))]//(t_(2)-t_(1)) (The average stands for average of the quantity over the time interval t_(1)" to "t_(2))
View Solution
