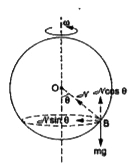
R त्रिज्यावाली वृत्त के रूप में मुदा एक पतला तार अपने ऊर्ध्वाधर व्यास (vertical diameter) के परितः कोणीय आवृत्ति ω से घूर्णन करता है (चित्र 1.6 - 8 ) सिद्ध करे कि यदि ω<√g/R तो इस तार में पिरोया हुआ कोई मोती अपने निम्नतम बिंदु A पर ही होगा। यदि ω=√2gR तो मोती को केंद्र O मिलानेवाली त्रैज्य रेखा OB ऊर्ध्वाधर से कितना कोण बनाएगी ? (घर्षण उपेक्षणीय माने)

मान लिया किकोणीय आवृत्ति ω के किसी मान के लिए मोती को केंद्र O से मिलनेवाले त्रिज्या OB ऊर्ध्वाधर के साथ θ कोण बनाती है (चित्र 1.6 - 9 ) + मोती पर लगनेवाले केवल दो बल होंगे (i) मोती का भार mg तथा (ii) तार द्वारा मोती पर अभिलंब प्रतिक्रिया N
अब N को ऊर्ध्वाधर तथा क्षैतिज दिशाओ को विघटित करने पर क्षैतिज घटक Nsinθ आवश्यक अभिकेंद्र बल प्रदान करेगा तथा ऊर्ध्वाधर घटक Ncosθ से मोती का भार (mg) संतुलित होगा।
∴Nsinθ=mω2r=mω2Rsinθ
या N=mω2R . . . (1) फिर Ncosθ=mg
mω2Rcosθ=mg [समीकरण (1) से ]
या cosθ=gω2R
अब चूँकि |cosθ|≤1 अतः gω2R≤1 या ω2Rg≥1
या ω≥√gR या ωmin=√gR
अतः ω का मान इस न्यूनतम मान (√gR) से कम होने पर मोती अपने न्यूनतम बिंदु A पर ही रहेगा।
यदि ω=√2gR तब cosθ=gω2R=g2g=12∴θ=60∘
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.7 आवेग एवं संवेग
20 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.8 द्रव्यमान केंद्र : घूर्णन
34 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.5 कार्य , शक्ति और ऊर्जा
33 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
1 kg तथा 16 kg द्रव्यमान के दो ब्लॉक की गतिज उर्जाएँ समान उनके रैखिक संवेग का अनुपात ज्ञात करे।
View SolutionHCI अणु के दो परमाणुओं (atoms) के नाभिक (nucleus) एक - दूसरे से लगभग 1.27Å की दुरी पर रहते है। इस अणु के द्रव्यमान - केंद्र की स्थिति ज्ञात करे। मान ले कि क्लोरीन का एक परमाणु हाइड्रोजन के परमाणु से 35.5 गुना भारी होता है तथा परमाणु का द्रव्यमान इसके नाभिक पर स्थिर होता है।
View Solutionकिसी वस्तु पर आरोपित बल द्वारा किया गया कार्य धनात्मक अथवा ऋणात्मक दोनों हो सकता है नीचे दिए गए प्रकथनो को ध्यानपूर्वक पढ़कर करणसहित बताएँ कि निम्नांकित कार्य धनात्मक है अथवा ऋणात्मक ?
रस्से से बंधी किसी बाल्टी को रस्सी द्वारा कुएँ से बाहर निकलने में किसी व्यक्ति द्वारा किया गया कार्य
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
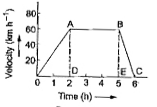
View Solutionयदि मूल बिंदु असामिका को संतुस्ट करता है तो छायांकित क्षेत्र रेखा के किस तरफ होगा ?
View Solutionयदि 1,ω,ω2 इकाई एक घनमूल हों, तो ∣∣∣1ωω−ω∣∣∣ का मान होगा -
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionयदि ω इकाई का एक घनमूल हो, तो सारणिक ∣∣ ∣ ∣∣1ω4ω8ω4ω81ω81ω4∣∣ ∣ ∣∣ का मान है-
View Solutionमाना ω एक सम्मिश्र संख्या ऐसी है कि 2ω+1=z जहाँ, z=√−3 है। यदि ∣∣ ∣ ∣∣1111−ω2−1ω21ω2ω2∣∣ ∣ ∣∣=3k है तो k बराबर है
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionयदि 1,omega,omega^2 इकाई के घनमूल हों, तो |(1,omega),(omega,-omega)| का मान होगा :
View Solutionयदि कोई जीवा वृत्त के केन्द्र से गुजरती है, तो उसे ........." कहते हैं।
View Solutionयदि सुलेखा रेलगाड़ी' को रेलगाडि' लिखती है तो एक भाषा-शिक्षक के रूप में आप क्या करेंगे?
View Solutionयदि 5m तार को 8 भागों में विभाजित करते है तो हर एक भाग की लम्बाई ज्ञात करो।
View Solution
