Question

If the diameter of circle bisects each of the two chords of the circle, then both the chords:
यदि वृत्त का व्यास वृत्त के दो जीवा
को बराबर हिस्सों में काटता है, तो दोनों जीवा:

Options

A. intersect at `90^@`
B. are parallel to each other
C. intersect at `30^@`
D. intersect at `60^@`

Explanation

To solve the problem, we need to analyze the situation where the diameter of a circle bisects two chords. Here’s a step-by-step solution:

Step 1: Understand the Circle and Chords
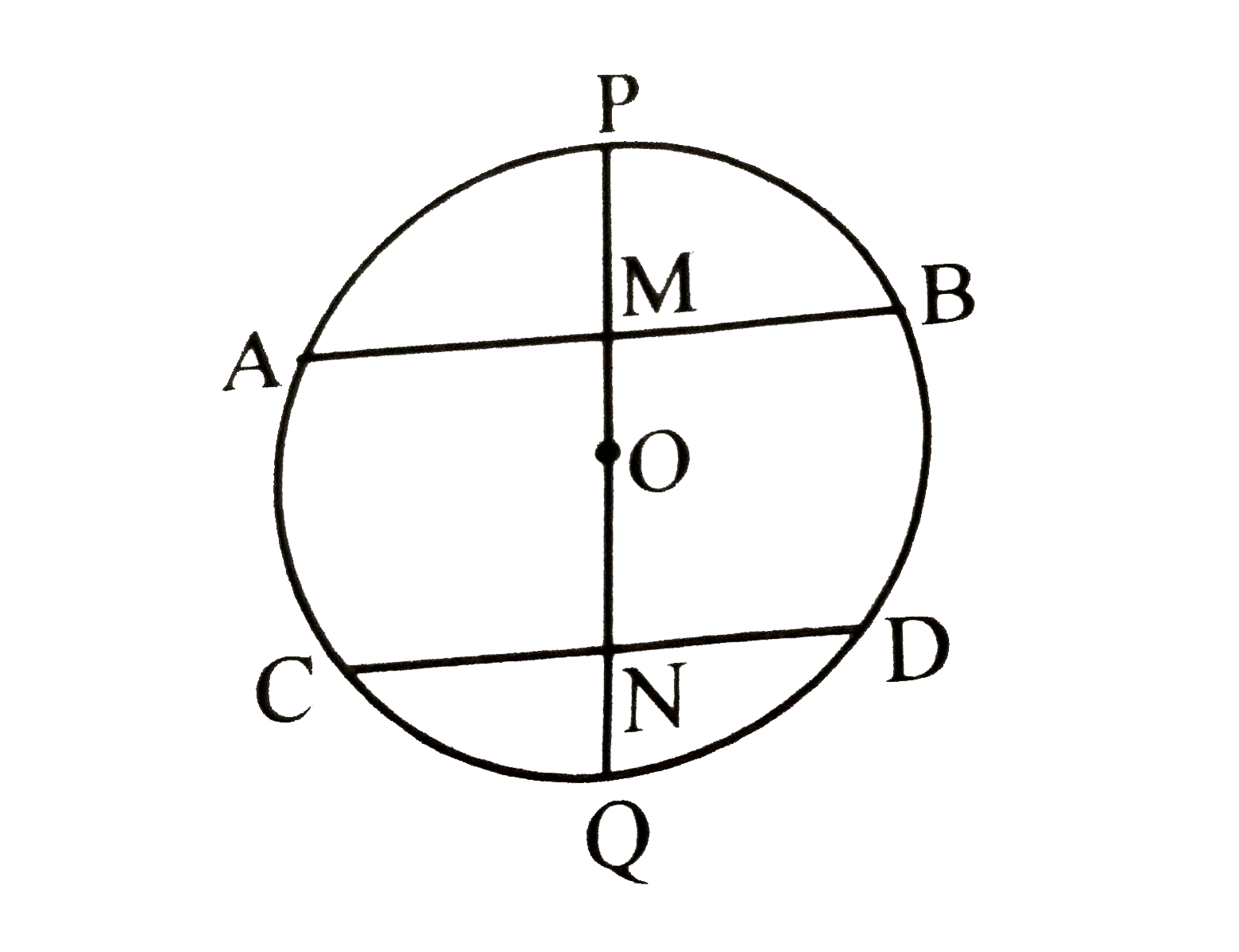
Let’s consider a circle with center O. We have two chords, AB and CD, and a diameter EF that passes through the center O and bisects both chords.

Step 2: Identify the Properties of the Circle
According to the properties of circles, a line drawn from the center of a circle that is perpendicular to a chord will bisect that chord. This means that if the diameter EF is perpendicular to both chords AB and CD, then it will divide each chord into two equal segments.

Step 3: Establish the Relationships
Since EF bisects both chords, we can denote the points where EF intersects AB and CD as M and N respectively. Thus, we have:
- AM = MB (AB is bisected)
- CN = ND (CD is bisected)

Step 4: Apply the Perpendicularity Property
Since EF is the diameter and is perpendicular to both chords, we can conclude that:
- OM ⊥ AB
- ON ⊥ CD

Step 5: Conclude the Relationship Between the Chords
From the property of circles, we know that if two chords are bisected by a diameter and are perpendicular to that diameter, then the chords must be parallel to each other. Therefore, we conclude that:
- Chord AB is parallel to chord CD.

Final Conclusion
Thus, if the diameter of a circle bisects each of the two chords of the circle, then both the chords are parallel to each other.

---