समान लंबाई की एक जैसी दो सीढ़ियों के एक सिरे पर कब्जा (hinges) लगाकर तथा इनके ठीक बीच में 50 cm लंबी रस्सी जोड़कर ऐसा बनाया गया है ताकि ये ऊर्ध्वाधरतः खड़ी रह सके (चित्र 1.8 - 14 )। प्रत्येक सीधी की लंबाई 1. 6 m है। एक सीढ़ी की लंबाई है। एक सीढ़ी के निचले सिरे B से सीढ़ी के अनुदिश 1.2 m की दुरी पर 40 kg का एक भार लटकाया गया है। यह मानते हुए कि फर्श एवं सीढ़ी के बीच घर्षण शून्य है तथा सीढ़ी पर भार नगण्य है, निम्नांकित के मान ज्ञात करे।
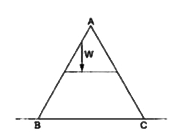
(a) रस्सी में तनाव , तथा
(b) सीढ़ी पर फर्श द्वारा आरोपित अभिलंब प्रतिक्रियाएँ (g=9.8ms−2)
चित्र 1.8 - 15 में प्रदर्शित निकाय अपनी व्यापक संतुलन की स्थिति में है जिसके अनुसार रैखिक स्थानातरीय संतुलन की शर्त (∑→F=0) तथा घूर्णन संतुलन की शर्त (→τ=0) साथ - साथ मान्य होगी।
मान लिया कि रस्सी DE में तनाव = T तथा फर्श के संपर्क बिंदु B तथा C पर अभिलंब प्रतिक्रियाएं क्रमशः N1 तथा N2 है। बिंदु P पर 40 kg द्रव्यमान का एक भार W निलंबित है जहाँ AP=40cm
प्रश्न से BC=2×DE=2×50cm=100cm
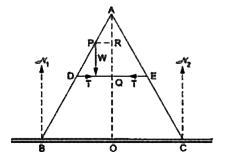
AO=√AB2−OB2=√(1.6m)2−(0.5m)2=1.5m
∴AQ=12AO=12×1.5m=0.75m
AR=12AQ=12×0.75m=0.375m
PR=12DQ=12×0.25m=0.125m
अब रैखिक स्थानातरीय संतुलन की शर्त से, ऊर्ध्वाधर दिशा में N1+N2−W=0
अतः N1+N2=W . . . (1)
फिर AB के घूर्णन संतुलन के लिए बिंदु A के परितः N1T तथा W बलों के आघूर्ण (torque) लेने पर
N1⋅OB−T⋅AQ−W⋅PR=0
या N1(0.5m)−T⋅(0.75m)−W⋅(0.125m)=0 . . . (2)
इसी प्रकार AC के घूर्णन संतुलन के लिए बिंदु A के परितः N2 एवं T के आघूर्ण लेने पर
N2⋅OC−T⋅AQ=0
या N2⋅(0.5m)−T(0.75m)=0 . . . (3)
समीकरण (2) एवं (3) के योगफल से,
(N1+N2)(0.5m)−2T(0.75m)−W(0.125m)=0
या W(0.5m−0.125m)=2T(0.75m) [∴N1+N2=W]
∴T=W2×(0.375m)0.75m=(40kg)(9.8ms−2)×0.3751.50=98N
अतः रस्सी में अभीष्ट तनाव = 98 N
समीकरण (3) में t का मान रखने पर N2=(98N)(0.75m)(0.5m)=147N
अतः समीकरण (1) से N1=W−N2=(40kg)(9.8ms−2)−147N=392N−147N=245N
अतः तनाव T=98N,N1=245N,N2=147N
Topper's Solved these Questions
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1. 9 गुरुत्वाकर्षण
25 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.10 प्रत्यास्थता
27 Videos
- सामान्य भौतिकीBOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.7 आवेग एवं संवेग
20 Videos
- सरल रेखा एवं समतल, में कण की गति BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)
24 Videos
Similar Questions
किसी विघुत आवेश को अन्य आवेशों के वैघुत बलों से परिरक्षित (shield ) करने के लिए उस आवेश को खोखले चालक के अंदर रखा जाता है । क्या किसी वस्तु को अन्य द्रव्यमान के गुरुत्वीय बलों से परिरक्षित करने के लिए उसे किसी खोखले गोले में रखकर या किसी अन्य साधन द्वारा ऐसा किया जा सकता है ?
View Solutionदो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।
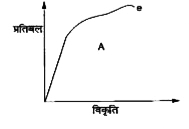
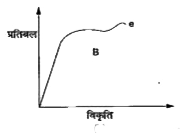
किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है ?
View Solution1 kg तथा 16 kg द्रव्यमान के दो ब्लॉक की गतिज उर्जाएँ समान उनके रैखिक संवेग का अनुपात ज्ञात करे।
View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
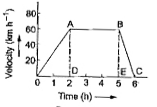
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View SolutionThe perimeter of a rectangle is 50 cm. Its area and length are in the ratio of 5:1. Find the length of the rectangle?
एक आयत की परिधि 50 सेमी है। इसका क्षेत्रफल और लंबाई 5: 1 के अनुपात में है। आयत की लंबाई ज्ञात कीजिये?
View SolutionA train moves at the speed of 80 km/h and crosses a platform in 0.75 minutes. If the length of the train is equal to the length of the platform, then what is the length of the platform?
एक ट्रेन 80 km/h की गति से चलती है और एक प्लेटफॉर्म को 0.75 मिनट में पार करती है। यदि ट्रेन की लंबाई प्लेटफ़ॉर्म की लंबाई के बराबर है, तो प्लेटफ़ॉर्म की लंबाई क्या है?
View SolutionThe length of the diagonal of a rectangle is 26 cm and one side is 10 cm. The area of the rectangle is:
एक आयत के विकर्ण की लंबाई 26 सेमी है तथा इसकी एक भुजा 10 सेमी की है | इस आयत का क्षेत्रफल है:
View SolutionLength and breadth of rectangular field are in the ratio 5 : 2. If the perimeter of the field is 238 m. Find the length of the field.
एक आयताकार मैदान की लंबाई और चौड़ाई 5 : 2 के अनुपात में है। यदि मैदान का परिमाप 238 मीटर है, तो मैदान की लंबाई ज्ञात कीजिए।
View SolutionTwo parallel chords are drawn in a circle of diameter 20 cm. The length of one chord is 16 cm and the distance between the two chords is 12 cm. The length of the other chord is : एक वृत्त में दो समानांतर जीवाओं को खींचा जाता है, जिसका व्यास 20 सेमी है। एक जीवा की लंबाई 16 सेमी है तथा दोनों जीवाओं के बीच की दूरी 12 सेमी है। दूसरी जीवा की लंबाई कितनी है?
View SolutionThe perimeter of a rectangle is 50 cm. Its area and length are in the ratio of 5:1. Find the length of the rectangle? एक आयत की परिधि 50 सेमी है। इसका क्षेत्रफल और लंबाई 5: 1 के अनुपात में है। आयत की लंबाई ज्ञात कीजिये?
View SolutionIn a circle of radius 13 cm , a chord is at a distance of 12 cm from the centre of the circle. What is the length of the chord?
13 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 12 सेमी की दूरी पर एक जीवा है | जीवा की लंबाई ज्ञात करें |
View SolutionIn a circle of radius 17 cm, a chord is at a distance of 15 cm from the centre of the circle. What is the length of the chord?
17 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 15 सेमी की टूरी पर एक जीवा है| जीवा की लंबाई ज्ञात करें |
View SolutionIn a circle of radius 17 cm, a chord is at a distance of 8 cm from the centre of the circle. What is the length of the chord?
17 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 8 सेमी की दूरी पर एक जीवा है | जीवा की लंबाई ज्ञात करें |
View Solution
