प्रमाणित करे कि किसी कण की सरल आवर्त - गति के एक पूर्ण दोलन में गतिज ऊर्जा एवं स्थितिज ऊर्जा के माध्य मान (average values ) समान होते है
सरल आवर्त गति में कण का तात्क्षणिक विस्थापन x=Asinωt
तथा तात्क्षणिक चाल v=dxdt=Aωcosωt.
समय t के फलन के रूप में कण की गतिज ऊर्जा KE=12mA2ω2cos2ωt
तथा स्थितिज ऊर्जा U=12mω2x2=12mω2A2sin2ωt
किसी फलन के माध्य मान की परिभाषा के अनुसार
x=a तथा x=b सीमांतो के बीच फलन f(x) का माध्य मान
[f(x)]av=1(b−a)∫baf(x)dx.
स्पष्टतः, एक संपूर्ण आवर्तकाल T के अंतराल में, KE एवं PE के माध्य मान,
(KE)av=1T∫T0mω2A2cos2ωt⋅dt=mω2A22T∫T0cos2ωtdt
=mω2A22T×2∫T02cos2ωtdt=mω2A24T∫T0(1+cos2ωt)dt
=mω2A24T[t+12ωsin2ωt]T0=14mω2A2
इसी प्रकार, (PE)av=1T∫T01.2mω2A2sin2ωt⋅dt
=mω2A22T×2∫T0(1−cos2ωt)dt
=mω2A24T[t−12ωsin2ωt]T0
=14mω2A2
अतः, एक पूर्ण दोलन में गतिज एवं स्थितिज ऊर्जाओं के माध्य मान =14mω2A2 तथा यह माध्य मान कुल यांत्रिक ऊर्जा =(=12mω2A2) का आधार है प्रमाणित ।
Topper's Solved these Questions
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.12 तरल दाब : पास्कल का नियम : पृष्ठ - तनाव19videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1 . 13 बरनूली - प्रमेय : श्यानता15videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.10 प्रत्यास्थता27videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)24videos
सरल रेखा एवं समतल, में कण की गति
Similar Questions
दो पात्रों (vessels) के आधारों के क्षेत्रफल समान है , परंतु आकृतियाँ (shapes) भिन्न - भिन्न है। पहले पात्र के दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है क्या दोनों प्रकरणो (cases) के पात्रो के आधारों पर आरोपित बल समान है ?
50:18View Solutionजब हम किसी जल - टोटी (water tap) को अपनी उँगलियों द्वारा बंद करने का प्रयास करते है , तो उँगलियों के बीच की खली जगह से तीव्र जल - धाराएँ फुट निकलती है। व्याख्या करे।
58:46View Solutionदो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।
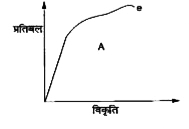
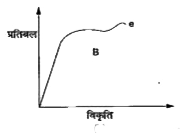
किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है ?41:08View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
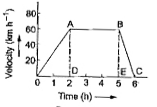 37:10View Solution
37:10View Solutionगतिज ऊर्जा तथा स्थितिज ऊर्जा | यांत्रिक ऊर्जा
39:53View Solutionऊर्जा के विभिन्न रूप | यांत्रिक ऊर्जा |गतिज ऊर्जा तथा स्थितिज ऊर्जा | संवेग और गतिज ऊर्जा में सम्बन्ध |किसी स्प्रिंग की स्थितिज ऊर्जा
51:53View Solutionदोलन|सरल आवर्त गति #!#सरल आवर्त गति में ऊर्जा
36:35View Solutionदोलन|सरल आवर्त गति #!#स्प्रिंग ब्लॉक निकाय के दोलन
35:21View Solutionदोलन|सरल आवर्त गति #!#स्प्रिंगब्लॉक निकाय के सरल आवर्त गति
46:06View Solutionसरल आवर्त गति में ऊर्जा|स्प्रिंग के दोलन
34:12View Solutionदोलन|सरल आवर्त गति #!#सरल लोलक के प्रकार
01:31:47View Solutionदोलन|सरल आवर्त गति #!#सरल लोलक के नियम
01:21:20View Solutionसरल आवर्त गति मे गतिज एवं स्थितिज ऊर्जा
01:22:02View Solutionतरलों के यांत्रिकी गुण |प्रवाहित तरल की ऊर्जा #!#गतिज ऊर्जा #!#स्थितिज ऊर्जा#!#दाब ऊर्जा
01:23:54View Solutionसरल आवर्त गति में ऊर्जा|सरल लोलक
01:20:22View Solutionसरल आवर्त गति में ऊर्जा
01:27:28View Solution

