10 kg द्रव्यमान की कोई ठोस डिस्क क्षैतिज स्थिति में अपने केंद्र से जुड़े किसी तार से ऊर्ध्वाधरतः लटक रही है । डिस्क को इसके अपने ही तल में तार एक परितः थोड़ा कोणीय विस्थापन देकर (अर्थात तार में ऐठन उत्पन्न कर ) छोड़ दिया जाता है जिससे निकाय मरोड़ी दोलन (torsional oscillation) निष्पन्न करने लगे। यदि दोलन का आवर्तकाल 1.5 s तथा डिस्क की त्रिज्या = 15 cm हो, तो तार का मरोड़ी नियतांक (torsional constant) ज्ञात करे [तार में θ ऐठन से उत्पान प्रत्यानयन टॉर्क τ∝−θ अर्थात τ=−αθ जहाँ α से मरोड़ी नियतांक , अर्थात ''प्रति एकांक ऐठन के लिए आवश्यक टॉर्क '' परिभाषित होता है ]
तार में अल्प ऐंठन θ के कारण नियंत्रक टॉर्क τ∝−θ अर्थात
τ=−αθ, जहाँ α= मरोड़ी नियतांक . . . (1)
घूर्णन के सिद्धांत से, τ=Idωdt . . . (2)
जहाँ I = ऊर्ध्वाधर अक्ष (अर्थात तार) के पारित डिस्क का जड़त्व - आघूर्ण तथा
ω= कंपन की कोणीय आवृत्ति =2πT.
∴ समीकरण (1) तथा (2) से, I⋅dωdt=−αθ
या कोणीय त्वरण, dωdt=−αI×θ . .. (3)
स्पष्टतः, कोणीय त्वरण ∝− कोणीय विस्थापन, अर्थात निकाय में कोणीय सरल आवर्त गति उत्पन्न हो रही है।
सिद्धांत से, त्वरण =−ω∧(2)× विस्थापन . . . (4)
समीकरण (3) तथा (4) से, ω2=αI
∴ मरोड़ी - नियतांक α=Iω2=I×(2πT)2=4π2T2×I=4π2T2×MR22
प्रश्न से, M = डिस्क का द्रव्यमान = 10 kg तथा R = त्रिज्या = 15 cm मान रखने पर, मरोड़ी - नियतांक का अभीष्ट मान
α=4×(3.14)2(1.5s)2×(10 kg)(15×10−2m)22=2 N m rad−1.
Topper's Solved these Questions
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.12 तरल दाब : पास्कल का नियम : पृष्ठ - तनाव19videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1 . 13 बरनूली - प्रमेय : श्यानता15videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सामान्य भौतिकीEXERCISE - 1.10 प्रत्यास्थता27videos
सामान्य भौतिकी
- BOOK - DAS GUPTACHAPTER - सरल रेखा एवं समतल, में कण की गति EXERCISE - प्रश्नावली (आंकिक प्रश्न)24videos
सरल रेखा एवं समतल, में कण की गति
Similar Questions
दो पात्रों (vessels) के आधारों के क्षेत्रफल समान है , परंतु आकृतियाँ (shapes) भिन्न - भिन्न है। पहले पात्र के दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दो गुना जल आता है क्या दोनों प्रकरणो (cases) के पात्रो के आधारों पर आरोपित बल समान है ?
02:48View Solutionजब हम किसी जल - टोटी (water tap) को अपनी उँगलियों द्वारा बंद करने का प्रयास करते है , तो उँगलियों के बीच की खली जगह से तीव्र जल - धाराएँ फुट निकलती है। व्याख्या करे।
05:14View Solutionदो पदार्थो A और B के लिए प्रतिबल - विकृति (stress-strain) ग्राफ चित्र 1.10-1 में दर्शाए गए है। इन ग्राफो को एक ही पैमाना (scale) मानकर खींचा गया है।
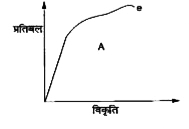
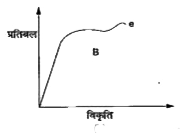
किस पदार्थ का यंग प्रत्यास्थता गुणांक अधिक है ?View Solutionएक बस का समय-वेग ग्राफ चित्र में दिखाया गया है। निम्नलिखित का मान निकालें-(i) किस समयांतराल में बस की चाल एकसमान है, (ii) किस समयांतराल में बस की गति त्वरित है, (ii) बस कुल कितनी दूरी चलती है, (iv) वह समयांतराल जिसमें बस की गति अवमंदित है तथा अवमंदन का मान क्या है?
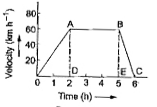 View Solution
View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionभुजंगा शाम को तार पर बैठकर पतिंगो को पकड़ता रहता है।
(मिश्र वाक्य में बदलिए)02:20View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है02:09View Solutionअपने से छोटों को पत्र में क्या संबोधन किया जाता है?
35:48View Solutionअपने से छोटों को पत्र में क्या संबोधन किया जाता है ?
05:43View Solutionयदि 5m तार को 8 भागों में विभाजित करते है तो हर एक भाग की लम्बाई ज्ञात करो।
03:18View Solutionएक 713 मीटर लम्बे तार को 7 बराबर भागों में काटा जाता है तब प्रत्येक भाग की लम्बाई होगी
02:02View Solutionचुंबकीय क्षेत्र में धारावाही तार
01:19View SolutionA solid sphere of brass with a radius 15 cm is drawn into a wire of diameter 6 mm. The length of the wire ( in cm ) is :
15 cm त्रिज्या वाले पीतल के एक ठोस गोले को 6 mm व्यास के तार में खिंचा जाता है | तार की लम्बाई (cm में) है:38:43View SolutionIf 3.96 cubic dm of lead is to be drawn in to a cylindrical wire of diameter 0.6 cm, then the length of the wire (in metres), is: यदि सीसा 3.96 घन डेसीमीटर है जिससे एक 0.6 सेमी व्यास के बेलनाकार तार को बनाना है, तो तार की लंबाई (मीटर में) है:
View SolutionA chord 10 cm long is drawn in a circle of diameter 26 cm. The perpendicular distance of the chord from the centre is: एक तार 10 सेमी लंबी, व्यास 26 सेमी के एक वृत्त में खींचा जाता है। केंद्र से जीवा की लंबवत दूरी है
View Solution

