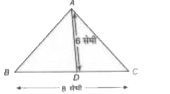
चित्र में, ti∠ABC की माध्यिका AD = 6 सेमी है। यदि आधार BC = 8 सेमी हो, तो AB + AC2 का मान है।
7 सेमी
−7सेमी
104 सेमी2
104 सेमी
The correct Answer is:D
Step by step video, text & image solution for चित्र में, tiangleABC की माध्यिका AD = 6 सेमी है। यदि आधार BC = 8 सेमी हो, तो AB + AC^(2) का मान है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - त्रिभुज EXERCISE - अभ्यास प्रश्न
17 Videos
- त्रिकोणमितीय फलनों के मान BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - त्रिकोणमितीय फलनों के मान EXERCISE - अभ्यास प्रश्न
18 Videos
- दो कोणों के योग एवं अन्तर के त्रिकोणमितीय फलन BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - दो कोणों के योग एवं अन्तर के त्रिकोणमितीय फलन EXERCISE - अभ्यास प्रश्न
19 Videos
Similar Questions
यदि किसी △ABC का O लम्बकेन्द्र, G केन्द्रक तथा S परिकेन्द्र है। तथा SG=3 सेमी हो, तो OG बराबर है।
View Solutionsin38212∘ का मान है
View Solutioncos20∘cos70∘−sin20∘sin70∘ का मान है
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View Solution
