ABC is a triangle. AB =10cm and BC=16 cm AD=8 cm and is perpendicular to side BC. What is the length (in cm) of side AC?
ABC एक त्रिभुज है। AB =10 सेमी तथा BC=16 सेमी है। AD=8 सेमी है तथा यह भुजा BC के समलम्ब है। भुजा AC का मान (सेमी. में) क्या है?
4√41
2√41
2√82
4√82
To find the length of side AC in triangle ABC, where AB = 10 cm, BC = 16 cm, and AD = 8 cm (with AD being perpendicular to BC), we can follow these steps:
Step 1: Identify the right triangle ABD
Since AD is perpendicular to BC, triangle ABD is a right triangle. Here, AB is the hypotenuse, AD is the perpendicular, and BD is the base.
Step 2: Apply the Pythagorean theorem in triangle ABD
According to the Pythagorean theorem:
AB2=AD2+BD2
Substituting the known values:
102=82+BD2
100=64+BD2
Step 3: Solve for BD
Rearranging the equation gives:
BD2=100−64
BD2=36
Taking the square root:
BD=√36=6 cm
Step 4: Find the length of DC
Since BC = 16 cm and BD = 6 cm, we can find DC:
DC=BC−BD=16−6=10 cm
Step 5: Identify the right triangle ADC
Now, we will use triangle ADC, which is also a right triangle. Here, AD is the perpendicular, DC is the base, and AC is the hypotenuse.
Step 6: Apply the Pythagorean theorem in triangle ADC
Using the Pythagorean theorem again:
AC2=AD2+DC2
Substituting the known values:
AC2=82+102
AC2=64+100
AC2=164
Step 7: Solve for AC
Taking the square root gives:
AC=√164
This can be simplified to:
AC=√4×41=2√41 cm
Conclusion
The length of side AC is 2√41 cm.
---
Since AD is perpendicular to BC, triangle ABD is a right triangle. Here, AB is the hypotenuse, AD is the perpendicular, and BD is the base.
According to the Pythagorean theorem:
AB2=AD2+BD2
102=82+BD2
100=64+BD2
Rearranging the equation gives:
BD2=100−64
BD2=36
Taking the square root:
BD=√36=6 cm
Since BC = 16 cm and BD = 6 cm, we can find DC:
DC=BC−BD=16−6=10 cm
Now, we will use triangle ADC, which is also a right triangle. Here, AD is the perpendicular, DC is the base, and AC is the hypotenuse.
Using the Pythagorean theorem again:
AC2=AD2+DC2
AC2=82+102
AC2=64+100
AC2=164
Taking the square root gives:
AC=√164
This can be simplified to:
AC=√4×41=2√41 cm
The length of side AC is 2√41 cm.
Topper's Solved these Questions
Similar Questions
M is the circumcentre of △ABC with circumradius 15 cm.Let BC = 24 cm and ML is perpendicular to BC. Then the length of ML is:
M त्रिभुज ABC का परिकेंद्र है, जिसकी परित्रिज्या 15 सेमी है। मान लीजिए कि BC = 24 सेमी है और ML, BC पर लम्ब है। तो ML की लंबाई ज्ञात कीजिए।
View SolutionIn △ABC,D is a point on BC such that AD is the bisector of ∠A, AB = 11.7 cm, AC = 7.8 cm and BC = 13 cm. What is the length (in cm) of DC?
त्रिभुज ABC में, D, BC पर स्थित एक ऐसा बिंदु है कि AD, ∠A का समद्विभाजक है |AB =11.7 सेमी, AC = 7.8 सेमी तथा BC =13 सेमी है | DC की लंबाई ( सेमी में ) कितनी है?
View SolutionABCD is a cyclic quadrilateral in which AB= 16.5 cm, BC = x cm, CD = 11 cm, AD= 19.8 cm and BD is bisected by AC at O. What is the value of x?/
ABCD एक चक्रीय चतुर्भुज है जिसमें AB = 16.5 सेमी, BC = x सेमी, CD = 11 सेमी, AD = 19.8 सेमी है तथा BD को AC के द्वारा O पर समद्विभाजित किया जाता है | x का मान क्या है ?
View SolutionIn △ABC ,∠C=90∘,AC = 5cm and BC = 12 cm. The bisector of ∠A meets BC at D. What is the length of AD?
△ABC में, ∠C=90∘ , AC = 5 सेमी तथा BC = 12 सेमी है | कोण A का समद्विभाजक BC से D पर मिलता है | AD की लंबाई कितनी है ?
View SolutionIf sides of a triangle are 12cm, 15 cm and 21 cm, then what is the in-radius (in cm) of the triangle?
यदि एक त्रिभुज को भुजाएँ 12 सेमी., 15 सेमी. तथा 21 सेमी है, तो त्रिभुज की अंत त्रिज्या (सेमी. में) क्या है?
View SolutionIn the given, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm2) of triangle PQR?
दी गई आकृति में , ABCDEF एक सम षट्भुज है जिसकी भुजा 12 से.मी.? है। P, Q तथा R क्रमशः भुजाओं AB, CD तथा EF के मध्य बिन्दु है। त्रिभुज PQR का क्षेत्रफल (से.मी.2 में) क्या है?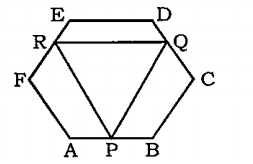
View SolutionIn △ABC ,D is a median from A to BC, AB = 6cm , AC =8cm and BC = 10cm The length of median AD (in cm ) is :
triangle ABC में, D, A से BC पर एक पर स्थित माध्यिका है।, AB = 6 सेमी, AC=8 सेमी और BC = 10 सेमी है। माध्यिका AD की लंबाई (सेमी में) है
View Solution△ABC is an equilateral triangle and AD⊥BC, where D lies in BC. If AD=4√3 cm, then what is the perimeter (in cm) of △ABC?
त्रिभुज ABC एक समबाह त्रिभुज है तथा AD bot BC है, जहाँ D, BC पर स्थित है | यदि AD= 4 sqrt3 सेमी है, तो त्रिभुज ABC का परिमाप ( सेमी में) कितना होगा ?
View SolutionIn a △ABC, the sides are AB= 16 cm, AC = 63cm, BC = 65cm. From A, a straight line AM is drawn up to the midpoint M of side BC. Then the length of AM is equal to :
त्रिभुज ABC में, AB = 16 सेमी, AC =63 सेमी, BC = 65 सेमी है | A से भुजा BC के मध्य बिंदु M तक एक सीधी रेखा AM खीची जाती है | AM की लंबाई ज्ञात करें |
View SolutionIn △ABC ,AC= 8.4 cm, BC= 14 cm. P is a point on AB such that CP = 11.2 cm and ∠ACP=∠B. What is the length (in cm) of BP?
△ABC में AC = 8.4 सेमी, BC = 14 सेमी है | P, AB पर स्थित एक ऐसा बिंदु है कि CP = 11.2 सेमी तथा ∠ACP=∠B है | BP की लंबाई (सेमी में ) कितनी है ?
View Solution
