संलग्न चित्र में प्रदर्शित तार में i ऐम्पियर धारा है। अर्द्ध-व्रत के केंद्र O पर चुंबकीय क्षेत्र क्या होगा (i) प्रत्येक ल लम्बाई के सीधे भाग के कारण, (ii) त्रिज्या a के अर्द्ध-वृत्त के कारण तथा (iii) पुरे तारे के कारण ?
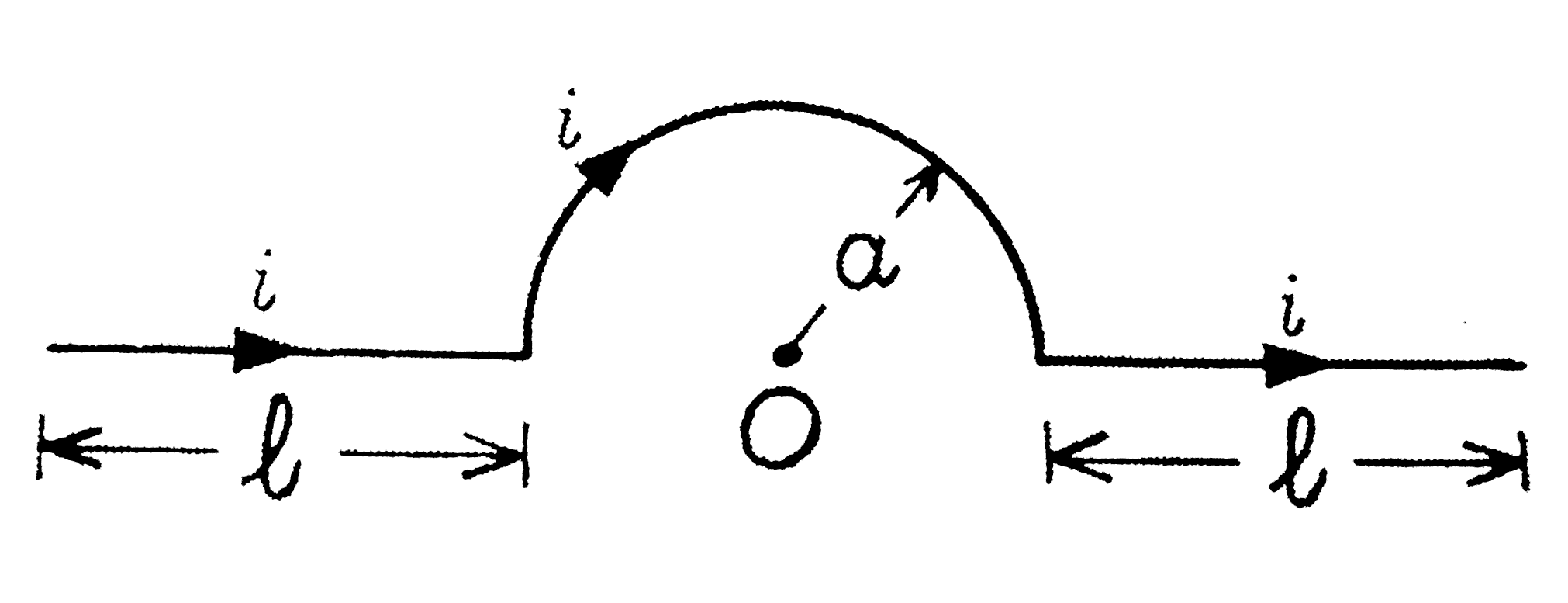
(i) बायो-सेवर्ट नियम से, धारावाही अवयव Δl से a दुरी पर स्थित पर चुंबकीय क्षेत्र
ΔB=μ04πIΔlsinθa2
जहाँ θअवयव Δ तथा अवयव को उस बिंदु से मिलाने वाली रेखा के बीच कोण है।
यहाँ तार के प्रत्येक सीधे भाग के लिए θ=0 (अथवा180∘) |
अतः प्रत्येक l लम्बाई के सीधे भाग के लिए
B1=B2=0
(ii) तार के अर्द्ध-वृत्त के कारण केंद्र पर चुंबकीय क्षेत्र B2=12(μ0i2a)=μ0i4a नीचे की ओर दिष्टि ।
(iii) पुरे तार के कारण चुंबकीय क्षेत्र B=B1+B2+B3=μ0i4aनीचे की ओर दिष्टि|
Topper's Solved these Questions
- गतिमान आवेश तथा चुंबकीय क्षेत्र Book:NOOTAN HINDIChapter:गतिमान आवेश तथा चुंबकीय क्षेत्र Exercise:प्रश्नावली (वस्तुनिष्ट प्रश्न)
Explore 41 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र Book:NOOTAN HINDIChapter:गतिमान आवेश तथा चुंबकीय क्षेत्र Exercise:अतिलघु उत्तरीय
Explore 84 Videos
- कॉलम का नियम तथा वैद्युत क्षेत्र Book:NOOTAN HINDIChapter:कॉलम का नियम तथा वैद्युत क्षेत्र Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 16 Videos
- चल कुण्डली धारामापी Book:NOOTAN HINDIChapter:चल कुण्डली धारामापी Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 15 Videos
Similar Questions
l लम्बाई के एक तर में i धारा प्रवाहित है । तार को मोड़ कर एक फेरे वाला वृत्तीय लूप बनाने पर, लूप के केंद्र पर उतपन्न चुंबकीय क्षेत्र B है । इस तार से 2 फेरों का लूप बनाये पर, लूप के केंद्र पर उत्पन्न चुंबकीय क्षेत्र होगा:
View Solutionबायो - सेवर्ट का नियम लिखिए तथा इसकी सहायता से विधुत धारा के S.I. मात्रक को परिभाषित कीजिए ।
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अंतर होता है। इनमे से एक −e है और दूसरा(e×Δe) है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो Δe कि कोटि होगी: (दिया है हाइड्रोजन का द्रव्यमान mh=1.67×10−27kg)
View Solutionआरेख में दण्ड (छड़) चुम्बको की व्यवस्थाओं के विन्यास दर्शाये गये है। प्रत्येक चुम्बक की द्विध्रुव आघूर्ण →M है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा?

View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र || कुछ प्रश्न
View Solutionकिसी बिन्दु-आवेश के कारण तथा आवेशों के निकाय के कारण विद्युत् क्षेत्र
View Solutionअनंत लंबाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र
View Solutionविद्युत् धारावाही पाश के कारण चुंबकीय क्षेत्र
View Solutionधारावाही वलय , पट्टिका के कारण चुंबकीय क्षेत्र
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionपरिनालिका के कारण चुंबकीय क्षेत्र
View Solutionपरिनालिका के कारण चुंबकीय क्षेत्र
View Solutionपरिनालिका के कारण चुंबकीय क्षेत्र
View Solutionवलय, अर्द्ध वलय आदि के कारण विद्युत क्षेत्र।
View Solution