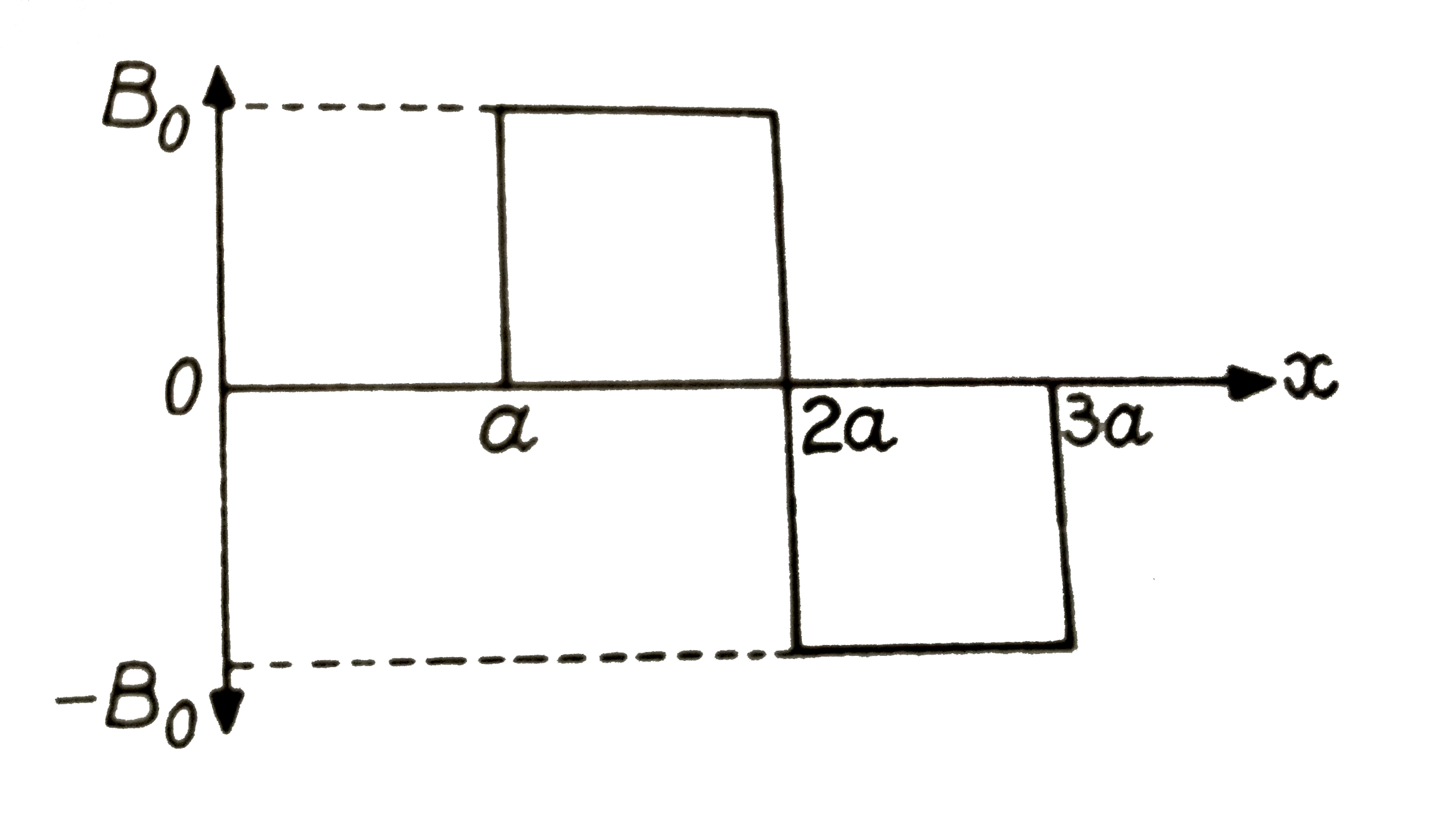
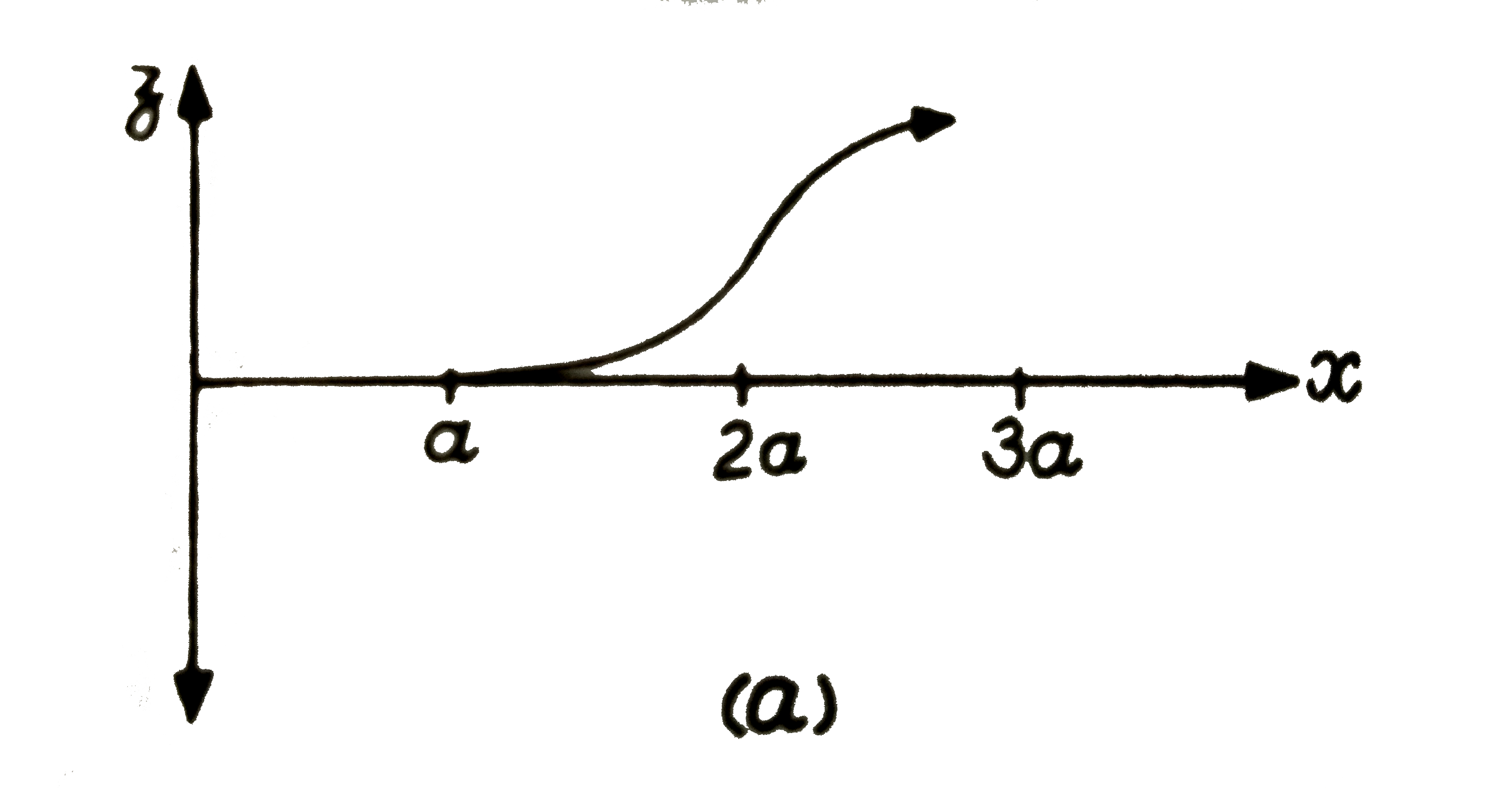
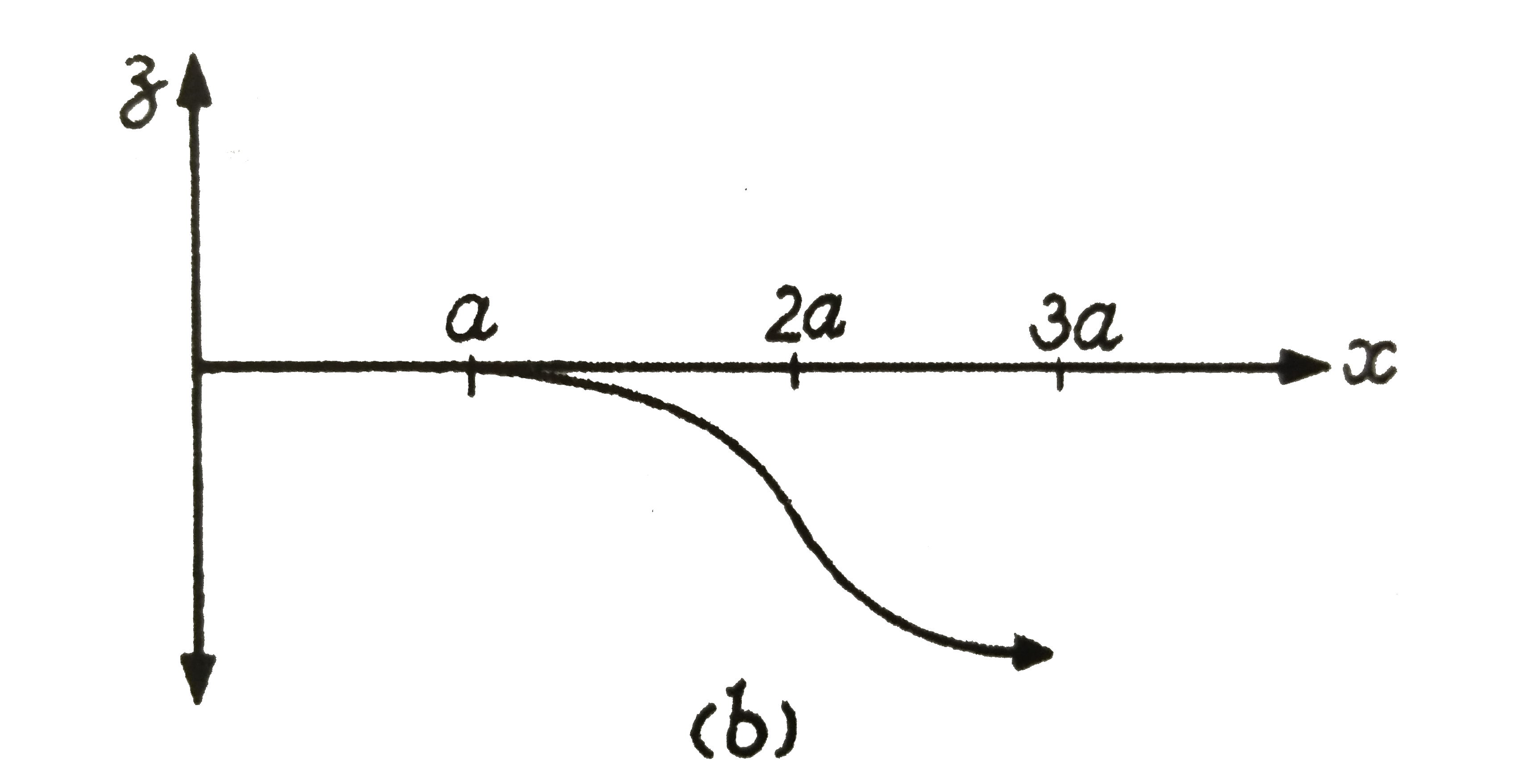
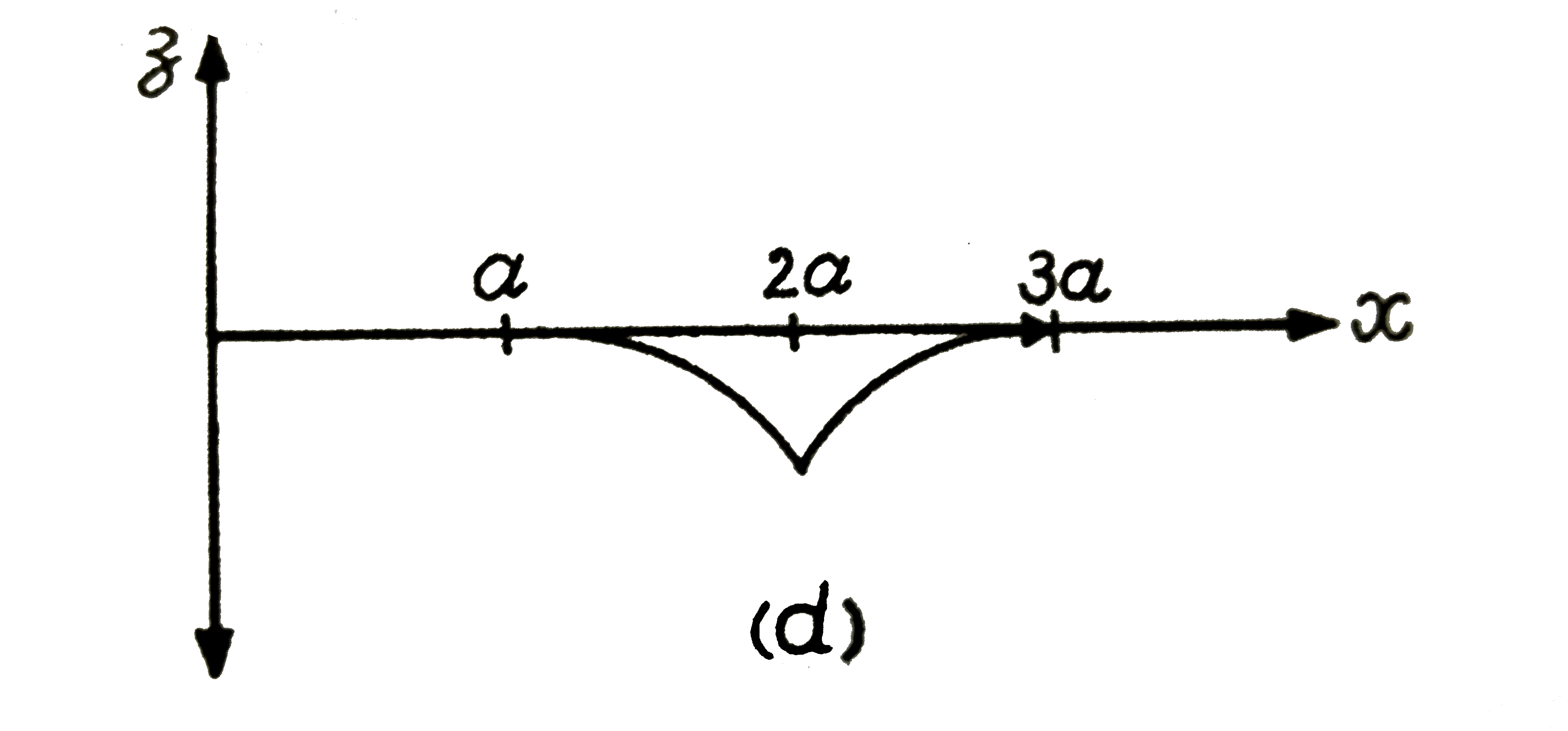
क्षेत्र a<x<2a में चुंबकीय क्षेत्र →B=B0ˆj है तथा क्षेत्र 2a>x>3aमें चुंबकीय क्षेत्र →B=−B0ˆj है, जहाँ B0 धनात्मक अचर है। वेग →v=v0ˆi जहाँ v0 धनात्मक अचर है, से चलता हुआ एक धनात्मक बिंदु-आवेश चुंबकीय क्षेत्र में x=a पर प्रवेश करता है। इस क्षेत्र में आवेश के पथ का सही निरूपण हो सकता है :
क्षेत्र altxlt2a में चुंबकीय क्षेत्र vecB=B(0)hatj है तथा क्षेत्र 2agtxgt3aमें चुंबकीय क्षेत्र vecB=-B(0)hatj है, जहाँ B(0) धनात्मक अचर है। वेग vecv=v(0)hati जहाँ v(0) धनात्मक अचर है, से चलता हुआ एक धनात्मक बिंदु-आवेश चुंबकीय क्षेत्र में x=a पर प्रवेश करता है। इस क्षेत्र में आवेश के पथ का सही निरूपण हो सकता है :

A

ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

क्षेत्र a<x<2aके लिए
→F=q(v0ˆi)×B0ˆj=qv0B0ˆK
अतः पथ ऊपर की और को अवतल होगा ।
क्षेत्र 2a<x<3aके लिए
→F=q(v0ˆi)×(−B0ˆj)=−qu0B0ˆk
अतः पथ नीचे की और अवतल होगा ।

Updated on:21/07/2023
|
Class 12PHYSICSMOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions