20 फेरो वाली एक वृत्ताकार कुण्डली का व्यास 8.0 सेमी है। इसमें 3.0 ऐम्पियर की धारा बह रही है। ज्ञात कीजिए : (i) कुण्डली का चुम्बकीय आघूर्ण, (ii) यदि कुण्डली को 0.50 न्यूटन/(ऐम्पियर-मीटर) के एकसमान चुम्बकीय क्षेत्र में इस प्रकार लटकाया जाये कि कुण्डली का तल चुम्बकीय क्षेत्र के समान्तर हो, तो उस पर लगने वाला बल-युग्म तथा (iii) यदि कुण्डली को चुम्बकीय क्षेत्र में स्वतन्त्रतापूर्वक लटका कर 108∘ के कोण से घुमाया जाये, तो किया गया कार्य।
(i) धारावाही कुण्डली का चुम्बकीय आघूर्ण (M), फेरों की संख्या N, धारा i तथा कुण्डली के क्षेत्रफल A की गुणा के बराबर होता है। इस प्रकार
M = N i A
प्रश्नानुसार, N = 20, I = 3.0 ऐम्पियर
तथा A=πr2=3.14×(4.0×10−2 मीटर)2
=5.0×10−3मीटर2
∴M=20×3.0 ऐम्पियर ×(5.0×10−3ऐम्पियर)
=0.30 ऐम्पियर- मीटर2|
(ii) जब किसी धारावाही कुण्डली को एकसमान चुम्बकीय क्षेत्र में →B इस प्रकार लटकाते है कि कुण्डली के तल पर केन्द्रीय अभिलम्ब (कुण्डली की अक्ष) क्षेत्र →B की दिशा से θ कोण बनाता है, तब इस पर लगने वाले बल-युग्म का मान
τ=MBsinθ
जब कुण्डली का तल चुम्बकीय क्षेत्र →B के समान्तर है अर्थात इसकी अक्ष →B क्षेत्र के लम्बवत है (θ=90∘ अथवा sinθ=1), तब बल-युग्म अधिकतम (τmax) होता है। इस प्रकार
τmax=MB
= 0.30 ऐम्पियर-मीटर2×0.50 न्यूटन/ (ऐम्पियर-मीटर)
=0.15 न्यूटन-मीटर।
(iii) चुम्बकीय क्षेत्र में लटकी धारावाही कुण्डली को θ कोण घुमाने में किया गया कार्य
W=MB(1−cosθ)
यदि कुण्डली को 180∘ घुमाया जाये, तब किया गया कार्य
W=MB(1−cos180∘)
=2MB=2×0.15 जूल = 0.30 जूल।
Topper's Solved these Questions
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - एन.सी.ई.आर.टी. प्रश्न
13 Videos
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - एन.सी.ई.आर.टी. प्रश्न (अतिरिक्त प्रश्न)
15 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
39 Videos
- तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतBOOK - NOOTAN HINDICHAPTER - तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतEXERCISE - वस्तुनिष्ट प्रकार प्रश्न ( एकल उत्तर प्रकार )
1 Videos
Similar Questions
तार की एक वृत्ताकार कुंडली में 100 फेरे है, प्रत्येक की त्रिज्या 8.0 सेमी है और इनमे 0.40 ऐम्पियर विघुत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुम्बकीय क्षेत्र का परिमाण क्या है?
View Solutionदो समकेंद्रिक वृत्ताकार कुंडलियाँ X और Y जिनकी त्रिज्याएँ क्रमशः 16 सेमी एवं 10 सेमी है, उत्तर-दक्षिण दिशा में समान ऊर्ध्वाधर तल में अवस्थित है। कुंडली X में 20 फेरे है और इसमें 16 ऐम्पियर विघुत धारा प्रवाहित हो रही है, कुंडली Y में 25 फेरे है और इसमें 18 ऐम्पियर विघुत धारा प्रवाहित हो रही है। पश्चिम की ओर मुख करके खड़ा एक प्रेक्षक देखता है कि X में धारा परवाह वामावर्त है जबकि Y में दक्षिणावर्त है। कुंडलियों के केंद्र पर, उनमे प्रवाहित विघुत धाराओं के कारण उतपन्न कुल चुंबकीय क्षेत्र का परिमाण एवं दिशा ज्ञात कीजिए।
View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
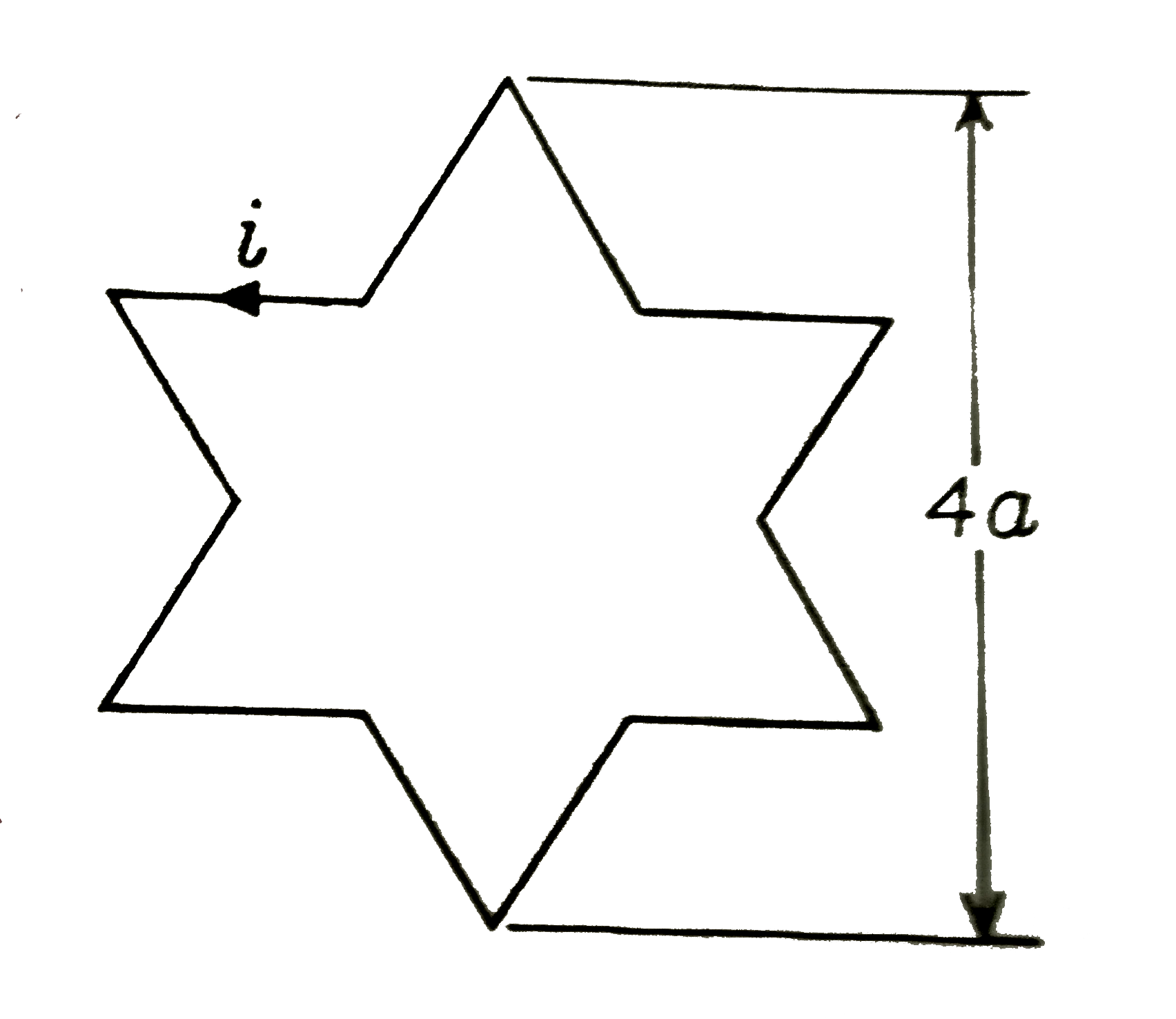
View Solutionग्रीष्म ऋतु की गर्म रात्रि में , भू-तल के निकट , वायु का अपवर्तनांक न्यूनतम होता है । और भू-तल से ऊंचाई के साथ बढ़ता जाता है । यदि , कोई प्रकाश - किरणपुँज क्षैतिज दिशा में जा रहा हो तो हाइगेन्स के सिद्धान्त से यह परिणाम प्राप्त होता है कि, चलते हुए प्रकाश किरणपुँज :
View Solutionएकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
View Solutionएकसमान चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव पर बल आधूर्ण तथा कार्य
View Solutionएक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल | संयुक्त विद्युत चुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionविद्युत धारावाही चालक पर चुंबकीय बल | दो समांतर विद्युत धाराओं के बीच बल-ऐम्पियर | एकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionचुम्बकीय द्विध्रुव तथा द्विध्रुव आघूर्ण | परिक्रमण करते इलेक्ट्रान का चुम्बकीय द्विध्रुव आघूर्ण | चुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionएकसमान चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव पर बल आधूर्ण तथा कार्य | पृथ्वी का चुम्बकीय क्षेत्र तथा अवयव | V,H तथा I में सम्बन्ध
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionएकसमान चुम्बकीय क्षेत्र में धारावाही कुंडली पर बल आघूर्ण
View Solutionगतिमान आवेश पर चुम्बकीय क्षेत्र के कारण लगने बल
View Solution
