1 सेमी लम्बाई के दो छोटे छड़-चुम्बक जिनके चुम्बकीय आघूर्ण क्रमश: 1.20 ऐम्पियर-मीटर2 तथा 1.00 ऐम्पियर-मीटर2 है। इन्हे एक क्षैतिज मेज पर परस्पर समान्तर इस प्रकार रखा जाता है कि उनके उत्तरी ध्रुव दक्षिण की ओर संकेत करें। उनकी चुम्बकीय निरक्ष उभयनिष्ठ है तथा परस्पर 20.0 सेमी की दूरी से पृथक्कृत है। उनके केन्द्रों को मिलाने वाली रेखा के मध्य बिन्दु O पर परिणामी क्षैतिज चुम्बकीय प्ररेणा लगभग है, (पृथ्वी का क्षैतिज चुम्बकीय प्ररेणा 3.6×10−5वेबर/मी2 है)
3.6×10−5 वेबर/मी2
2.56×10−4 वेबर/मी2
3.50×10−4 वेबर/मी2
5.80×10−4 वेबर/मी2
The correct Answer is:B
Bnet=B1+B2+BH
B1=μ04π×M[l2+y2]3/2
10−7×1.20[(0.005)2+(0.1)2]3/2
=10−7×1.20(10)−3
=1.20×10−4 वेबर/मी2 (दक्षिण से उत्तर की ओर)
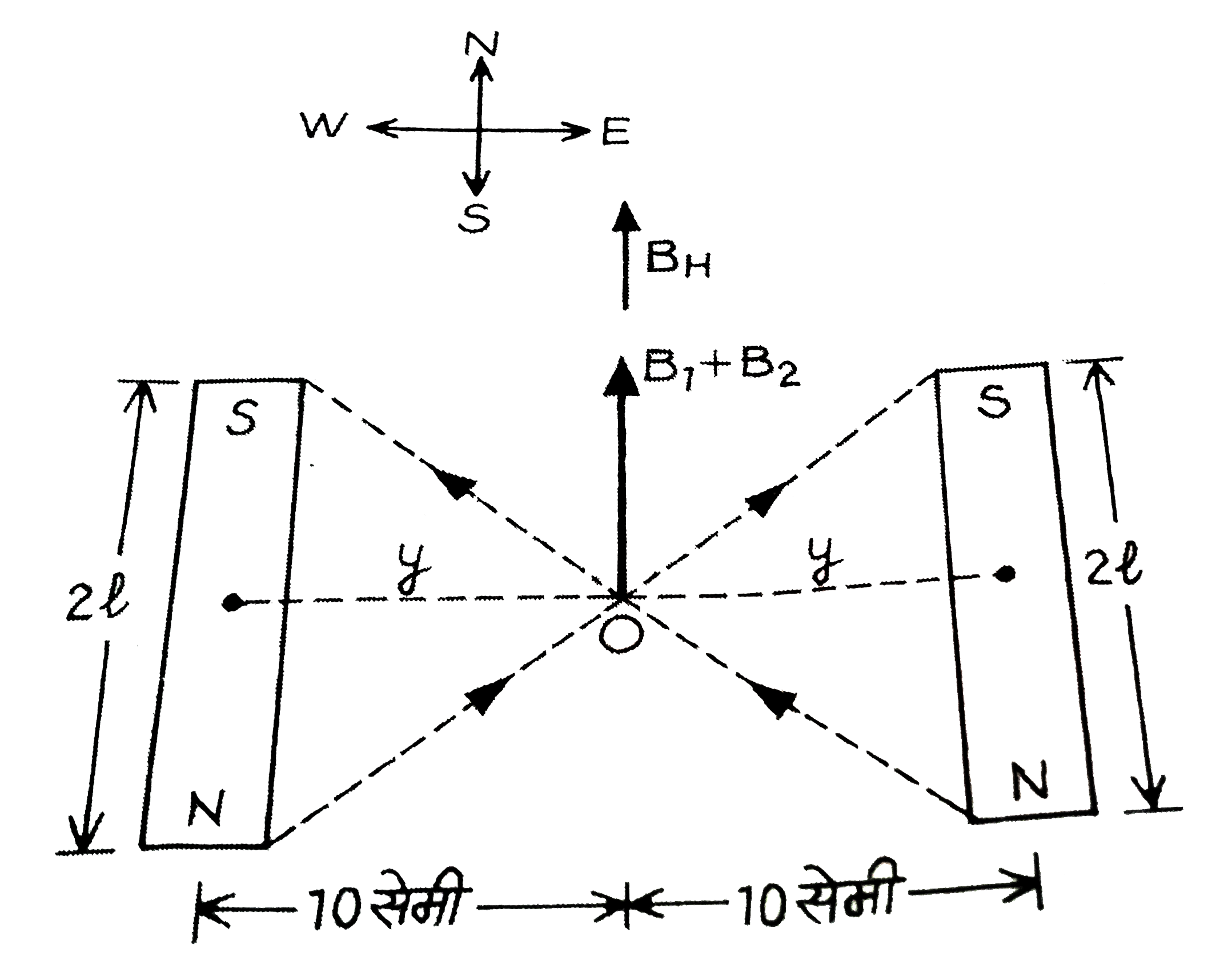
B2=1.00×10−4 वेबर/मी2 (दक्षिण से उत्तर की ओर)
BH=3.6×10−5 वेबर/मी2 (दक्षिण से उत्तर की ओर)
Bnet=(1.20+1.00+0.36)10−4 वेबर/मी2
=2.56×10−4 वेबर/मी2
Topper's Solved these Questions
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - आंकिक
37 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
39 Videos
- तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतBOOK - NOOTAN HINDICHAPTER - तरंग प्रकाशिकी तथा हाइगेन्स का सिद्धांतEXERCISE - वस्तुनिष्ट प्रकार प्रश्न ( एकल उत्तर प्रकार )
1 Video
Similar Questions
20 फेरों के एक कुण्डली का क्षेत्रफल 1.5 सेमी2 है तथा इसमें 3 ऐम्पियर की धारा बह रही है। यदि कुण्डली को 0.5 वेबर/मीटर2 के एकसमान चुम्बकीय क्षेत्र में इस प्रकार लटकाया जाए की कुण्डली का तल चुम्बकीय क्षेत्र के समान्तर हो, तो उस पर लगने वाले बल-युग्म का आघूर्ण ज्ञात कीजिए।
View Solutionजैसे की चित्रित किया गया है। एक सम्मित तारे (symmetric star)के आकार के चालक में अपरिवर्तित धरा ी बह रही है। यहाँ विपरीत शीर्षों (diametrically opposoite vertices) के बीच की दुरी 4a है। चालक के केंद्र पर चुंबकीय क्षेत्र का मान होगा :
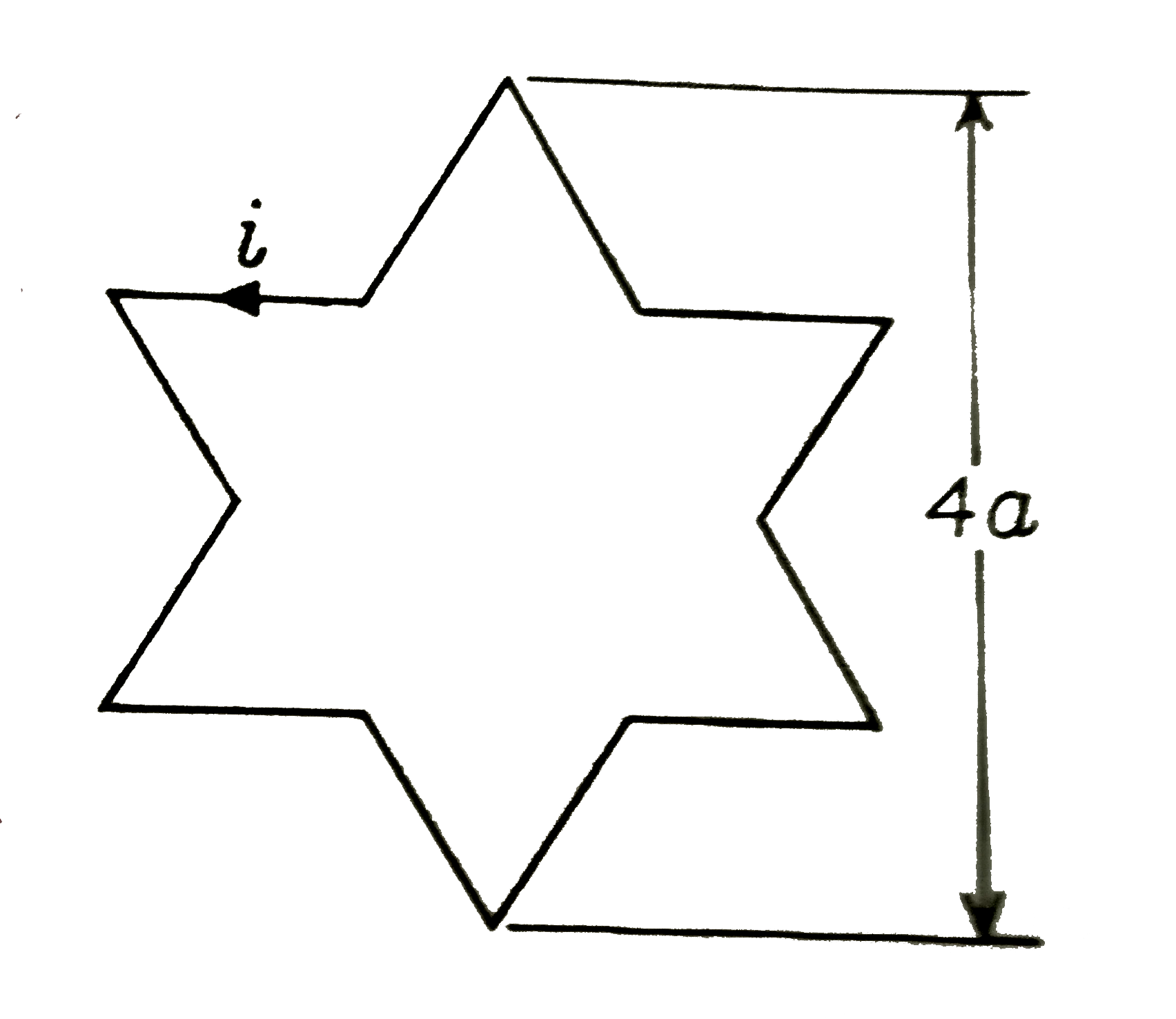
View Solutionग्रीष्म ऋतु की गर्म रात्रि में , भू-तल के निकट , वायु का अपवर्तनांक न्यूनतम होता है । और भू-तल से ऊंचाई के साथ बढ़ता जाता है । यदि , कोई प्रकाश - किरणपुँज क्षैतिज दिशा में जा रहा हो तो हाइगेन्स के सिद्धान्त से यह परिणाम प्राप्त होता है कि, चलते हुए प्रकाश किरणपुँज :
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 2.5 सेमी एवं 1.5 सेमी है जिनके केंद्र 8 सेमी दूरी पर स्थित है ,पर एक उभयनिष्ठ तिर्यक स्पर्श रेखा किन रचना कीजिए।
View Solutionदो वृत्त जिसकी त्रिज्याएँ 3 सेमी एवं 4 सेमी है। जिनके केन्द्रो के बाध्य की दूरी 8 सेमी है। दोनों वृतो पर उभयनिष्ठ स्पर्श रेखाएं कीतिनि खींची जा सकती है ?तथा दो उभयनिष्ठ अनुस्पर्श रेखाओ की रचना कीजि।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionदो वृत्त जिनकी त्रिज्याएँ 4 सेमी और 3 सेमी है तथा दोनों के केन्द्रो कि मध्य दूरी 6.5 सेमी हैकि रचना कर उन पर एक उभयनिष्ठ अनुस्पर्श रेखा कि रचना कीजिए।
View Solutionदो वृत्त 2.5 सेमी एवं 1 सेमी त्रिजियो के केंद्र परस्पर 7 सेमी दूरी पर है। एक उभयनिष्ठ तिर्यक स्पर्श रेखा कि रचना कीजिए।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution
