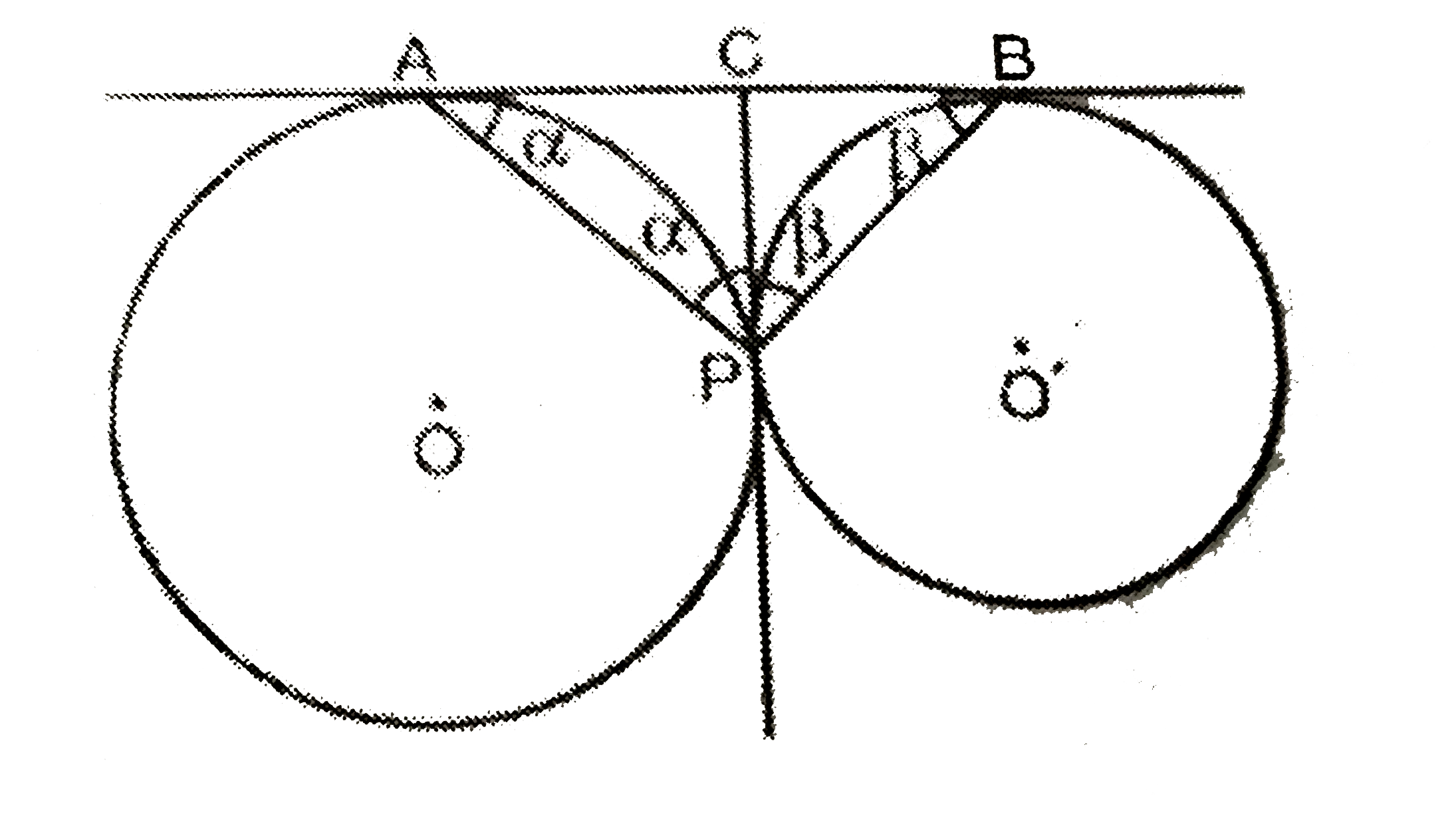
दो वृत्तों के केन्द्र O और O ' है, जो एक-दूसरे को बाहृतः बिन्दु P पर स्पर्श करते है। इन वृत्तों की एक उभयनिष्ट अनुस्पर्श रेखा AB खींची जाती है। सिद्ध कीजिए कि ∠APB=90∘.
दोनों वृत्त के स्पर्श बिन्दु P पर उभयनिष्ट स्पर्श रेखा PC खींची जो AB को बिन्दु C पर कटती है।
∴ CA और CP बाह्र्य बिन्दु C से केन्द्र O वाले वृत्त पर दो स्पर्श रेखाएँ है।
∴CA=CP
ΔACP समद्विबाहु त्रिभुज है जिसमे
∠PAC=∠APC=α
(माना)
इसी प्रकार CB=CP
∴ΔBCP समद्विबाहु त्रिभुज है जिसमे
∠PBC=∠BPC=β (माना)
अतः ΔAPB में, α+(α+β)+β=180∘ , (चित्र से)
या 2α+2β=180∘
या 2(α+β)=180∘
या α+β=90∘
या ∠APB=(anlpa+β)=90∘.
Topper's Solved these Questions
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(A)
4 Videos
- वृत्तBOOK - MANOHAR RAYCHAPTER - वृत्तEXERCISE - प्रश्नावली 10(B)
13 Videos
- वास्तविक संख्याएँ BOOK - MANOHAR RAYCHAPTER - वास्तविक संख्याएँ EXERCISE - प्रश्नावली 1(E)
25 Videos
- वृत्तों से संबंधित क्षेत्रफल BOOK - MANOHAR RAYCHAPTER - वृत्तों से संबंधित क्षेत्रफल EXERCISE - प्रश्नावली 12(D)
17 Videos
Similar Questions
रिक्त स्थानो की पूर्ति कीजिए :
(i) किसी वृत्त की स्पर्श रेखा उसे …………… बिन्दु पर प्रतिच्छेद करती है।
(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को …………… कहते है।
(iii) एक वृत्त की …………… समांतर स्पर्श रेखाएँ हो सकती है।
(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ट बिन्दु को ............ कहते है।
View Solutionसिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींची गया लम्ब वृत्त के केन्द्र से होकर जाता है।
View Solutionनिन्मलिखित में से परिमेय संख्याएँ छाँटकर लिखिए: √3,π3,2273√4,√414 और 2.33
View Solutionएक वृत्ताकार मार्ग के बाहरी और भीतरी व्यास क्रमश: 8 मीटर और 6 मीटर है। उसके दोनों तरफ तार खींचा जाये तो उसकी लम्बाई होगी :
View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्त एक दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ की संख्या लिखिये।
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionवक्र y=x2−5x+5 की स्पर्श रेखा, जो रेखा 2y=4x+1 के समांतर है, निम्न में से किस बिन्दु से होकर जाती है
View Solution
