In a circle with centre O, PQR is a tangent at the point Q on it. AB is a chord in the circle parallel to the tangent such that ∠BQR=70∘. What is the measure of ∠AQB ?
केंद्र O वाले एक वत्त में, PQR इस पर स्थित बिंदु Q पर एक स्पर्श रेखा है | AB वृत्त में एक जीवा है जो स्पर्श रेखा से इस प्रकार समानांतर है कि ∠BQR=70∘ है | ∠AQB का मान ज्ञात करें |
40∘
60∘
55∘
35∘
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry
We have a circle with center O, a tangent line PQR at point Q, and a chord AB that is parallel to the tangent. We know that angle BQR = 70°.
Step 2: Identify the Angles
Since AB is parallel to the tangent PQR, we can use the property of alternate interior angles. Therefore, angle AQB will be equal to angle BQR.
Step 3: Apply the Alternate Interior Angles Theorem
Since AB is parallel to PQR, we can state:
- angle BQR = angle AQB
Step 4: Substitute the Known Value
We know from the problem statement that:
- angle BQR = 70°
Thus, we can conclude:
- angle AQB = 70°
Step 5: Conclusion
The measure of angle AQB is 70°.
Final Answer
The measure of angle AQB is 70°.
---
We have a circle with center O, a tangent line PQR at point Q, and a chord AB that is parallel to the tangent. We know that angle BQR = 70°.
Since AB is parallel to the tangent PQR, we can use the property of alternate interior angles. Therefore, angle AQB will be equal to angle BQR.
Since AB is parallel to PQR, we can state:
- angle BQR = angle AQB
We know from the problem statement that:
- angle BQR = 70°
- angle AQB = 70°
The measure of angle AQB is 70°.
The measure of angle AQB is 70°.
Topper's Solved these Questions
Similar Questions
किसी बिंदु पर स्पर्श रेखा तथा अभिलंब
View SolutionPAT is a tangent to a circle at a point A on it , and AB is a chord such that, ∠BAT=72∘. If C is a point on the circle such that ∠CBA=58∘, then what is the measure of ∠CAB ?
PAT एक वृत्त के बिंदु A से इस पर खींची गयी स्पर्श रेखा है तथा AB एक ऐसी जीवा है कि ∠BAT=72∘ यदि C वृत्त पर स्थित ऐसा बिंदु है कि ∠CBA=58∘ है, तो ∠CAB का मान ज्ञात करें |
View Solution
Knowledge Check
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR=70∘ then ∠AQB is equal to
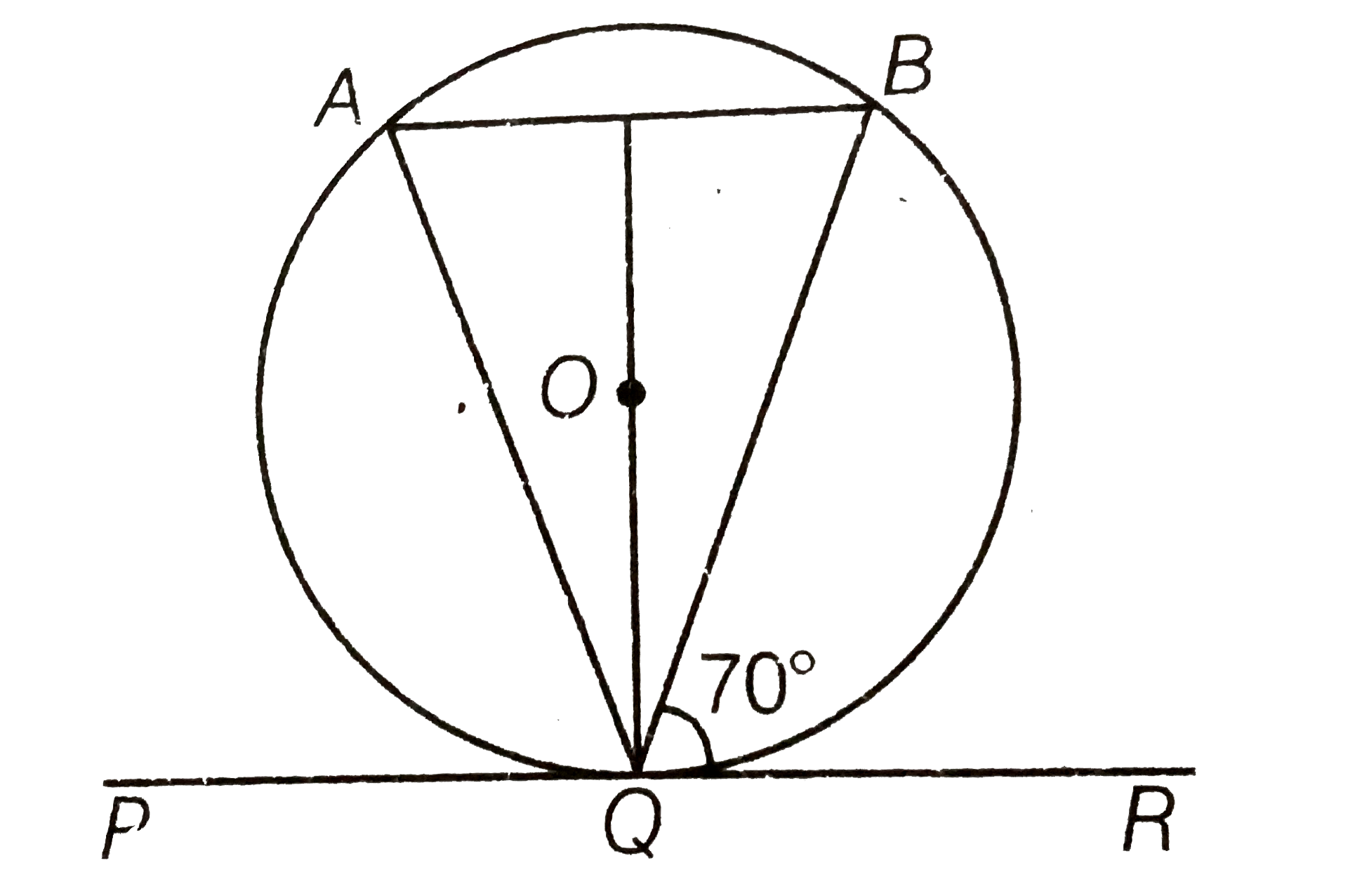 A20∘B40∘C35∘D45∘
A20∘B40∘C35∘D45∘
PRT is a tangent to a circle with centre O, at the point R on it. Diameter SQ of the circle is produced to meet the tangent at P and QR is joined. If ∠QRP=28∘, then the measure of ∠SPR is: /
PRT एक वृत्त, जिसका केंद्र O है, पर स्थित बिंदु R से जाने वाली स्पर्श रेखा है | वत्त के व्यास SQ को बढ़ाया जाता है जो स्पर्श रेखा से P पर मिलता है तथा QR को मिलाया जाता है | यदि ∠QRP=28∘ है तो ∠SPR का मान क्या होगा ?
View SolutionIn a circle with centre O, BC is a chord. Point D and A are on the circle, on the opposite side of BC, such that ∠DBC=28∘ and BD=DC. What is the measure of ∠BOC?
O केंद्र वाले एक वृत्त में, BC एक जीवा है। बिंदु D और A, वृत्त पर स्थित है जो BC के विपरीत है जैसे कि ∠DBC=28∘ और BD = DC। ∠BOC का माप कया है
View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB=142∘, then ∠OAB is equal to:
PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि ∠APB=142∘ है, तो ∠OAB का मान ज्ञात करे
View SolutionIn a circle with centre O, ABDC is a cyclic quadrilateral with AB as a diameter of the circle. AC and BD produced meet at E. If ∠CED=70∘, then what is the measure of ∠COD?
केंद्र O वाले एक वृत्त में, ABDC एक चक्रीय चतुर्भुज है जिसमें AB वृत्त का व्यास है| AC और BD को बढ़ाया गया है जो E पर मिलते हैं | यदि ∠CED=70∘ है, तो ∠COD का मान ज्ञात करें |
View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that ∠APB=80∘, then ∠OAB is equal to:
PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि ∠APB=80∘ है, तो ∠OAB का मान क्या होगा ?
View SolutionO is the centre of a circle to which PAX and PBY are tangents from a point P at points A and B. Q is a point on the circle ,such that ∠QAX=49∘, and ∠QBY=62∘ .What is the measure of ∠AQB ?
O एक वृत्त का केंद्र है जिस पर PAX और PBY स्पर्श रेखाएं हैं जो बिंदु P से A और B पर खींची गयी हैं | Q, वृत्त पर स्थित एक बिंदु है जो इस प्रकार है कि ∠QAX=49∘, और ∠QBY=62∘ है | ∠AQB का मान क्या है ?
View SolutionIn a circle with centre O, a diameter AB is produced to a point P lying outside the circle and PT is a tangent to the circle at the point C on it, If ∠BPT=36∘, then what is the measure of ∠BCP ?
O केंद्र वाले एक वृत्त में, एक व्यास AB को वृत्त के बाहर स्थित एक बिंदु P तक बढ़ाया जाता है और PT उस बिंदु C पर वृत्त के स्प्शरिखा है, यदि ∠BPT=36∘ है, तो ∠BCP का माप क्या है?
View Solution
