सिद्ध कीजिए कि
2tan−115+sec−15√27+2tan−118=π4
Video Solution
Text Solution
माना sec−15√27=θ
⇒secθ=5√77
इसलिए cosθ=75√2
तथा tanθ=17 ∴θ=tan−117
माना बायाँ पक्ष =2(tan−115+tan−118)+tan−117
=2tan−1⎡⎢
⎢⎣(15+18)1−15×18⎤⎥
⎥⎦+tan−117
2tan−1[1340×4039]+tan−117
=2tan−113+tan−117
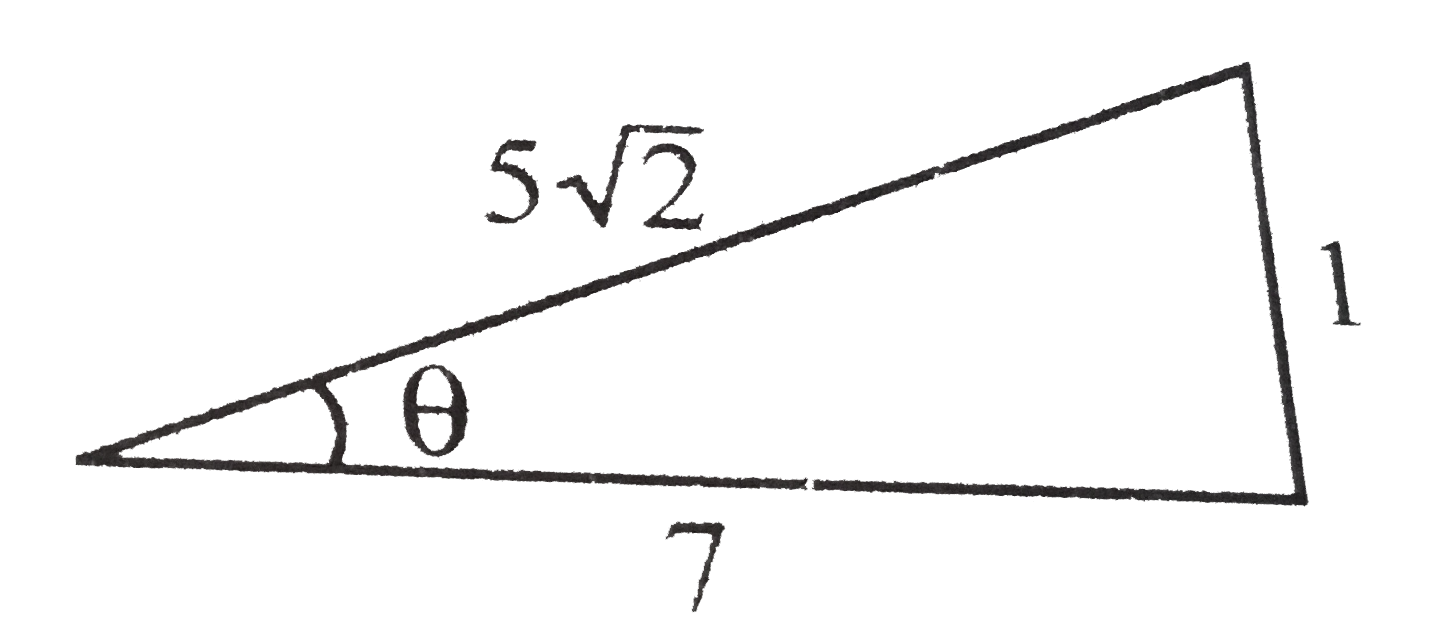
tan−1⎡⎢
⎢
⎢⎣2×131−(13)2⎤⎥
⎥
⎥⎦+tan−117
tan−134+tan−117
tan−1(34+17)(1−34×17)
=tan−12525=1=π4= दायाँ पक्ष
|
Topper's Solved these Questions
- प्रतिलोम त्रिकोणमितीय फलनBOOK - BALAJI PUBLICATIONCHAPTER - प्रतिलोम त्रिकोणमितीय फलनEXERCISE - अभ्यास प्रश्न 3.1
51 Videos
- प्रतिलोम त्रिकोणमितीय फलनBOOK - BALAJI PUBLICATIONCHAPTER - प्रतिलोम त्रिकोणमितीय फलनEXERCISE - अतिलघु उत्तरीय प्रश्न
40 Videos
- प्रतिलोम त्रिकोणमितीय फलनBOOK - BALAJI PUBLICATIONCHAPTER - प्रतिलोम त्रिकोणमितीय फलनEXERCISE - स्वमूल्यांकन परीक्षण
34 Videos
- निहित फलनों का अवकलन BOOK - BALAJI PUBLICATIONCHAPTER - निहित फलनों का अवकलन EXERCISE - स्वमूल्यांकन परिक्षण
32 Videos
- प्रतिस्थापन व्दारा समाकलन BOOK - BALAJI PUBLICATIONCHAPTER - प्रतिस्थापन व्दारा समाकलन EXERCISE - स्वमूल्यांकन परीक्षणं
27 Videos
Similar Questions
मान ज्ञात कीजिए -
sec−1(−√2)
View Solutionsin−1(sinπ3) का मान ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि tan−11+tan−112+tan−113=π4
View Solutionनिम्नलिखित प्रश्न में dydx ज्ञात कीजिये| y=tan−1(3x−x31−3x2),−1√3<x<1√3
View Solutionsinxsin(cosx) का समाकलन कीजिए -
View SolutionProve that 2tan−1(15)+sec−1(5√27)+2tan−1(18)=π4.
View SolutionProve the following: 4tan−115−tan−1170+tan−1199=π4 2tan−115+sec−15√27+2tan−118=π4
View SolutionProve that :2tan−1(15)+sec−1(5√27)+2tan−1 18=π4
View Solutiontan(2tan−1 15−π4)+717=0
View Solutionसिद्ध कीजिए -
2tan−1(15)+sec−1(5√27)+2tan−1.18=π4
View Solution2tan^(-1)(1/2)-tan^(-1)(1/7)=(pi)/(4)
View Solutionसिद्ध कीजिए कि 2tan−115+tan−117+2tan−118=π4
View Solution2Tan−115+Sec−15√27+Tan−118=
View Solutionसिद्ध कीजिए
2tan−1.12−tan−1.17=π4
View SolutionProve the following: 4tan−115−tan−1170+tan−1199=π4 2tan−115+sec−15√27+2tan−118=π4
View Solution