सिद्ध कीजिए कि समस्त त्रिभुजों के समुच्चय A में,R={(T1,T2):T1,T2 के समरूप है } द्वारा परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है । भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T1,भुजाओं 5, 12, 13 वाले समकोण त्रिभुज T2 तथा भुजाओं 6, 8, 10 वाले समकोण त्रिभुज T3 पर विचार कीजिए | T1,T2 और T3में से कौन-से त्रिभुज परस्पर सम्बन्धित हैं ?
यहाँ A≡ समस्त त्रिभुजों का समुच्चय
तथा R={(T1,T2):T1,T2के समरूप है }
∵ प्रत्येक त्रिभुज स्वयं के समरूप होता है
∴R स्वतुल्य है ।
माना T1,T2∈A तथा (T1,T2)∈R
⇒T1,T2 के समरूप है ।
⇒T2,T1 के समरूप है ।
⇒(T2,T1)∈R
∴R सममित है ।
माना T1,T2,T3∈A
तथा (T1,T2)∈R और (T2,T3)∈R
⇒T1,T2के समरूप है और T2,T3 के समरूप है ।
⇒T1,T3 के समरूप है ।
⇒(T1,T3)∈R
∴R संक्रमक है ।
∵R स्वतुल्य, सममित और संक्रमक है
∴R एक तुल्यता सम्बन्ध है । यही सिद्ध करना था ।
अब 36=48=510=12
⇒T1 और T3की संगत भुजायें समान अनुपात में हैं ।
अतः T1 और T3 समरूप हैं ।
⇒ त्रिभुज T1, त्रिभुज T3 से सम्बन्धित है ।
Topper's Solved these Questions
- सम्बन्ध एवं फलन Book:NOOTAN HINDIChapter:सम्बन्ध एवं फलन Exercise:एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.2))
Explore 12 Videos
- सम्बन्ध एवं फलन Book:NOOTAN HINDIChapter:सम्बन्ध एवं फलन Exercise:एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.3))
Explore 14 Videos
- सम्बन्ध एवं फलन Book:NOOTAN HINDIChapter:सम्बन्ध एवं फलन Exercise:प्रश्नावली (1E) (विविध प्रतियोगी परीक्षाओं हेतु प्रश्न )
Explore 10 Videos
- समाकलनो के अनुप्रयोग Book:NOOTAN HINDIChapter:समाकलनो के अनुप्रयोग Exercise:विविध प्रश्नवली
Explore 19 Videos
- सारणिकBook:NOOTAN HINDIChapter:सारणिकExercise:विविध प्रश्नावली
Explore 19 Videos
Similar Questions
सिद्ध कीजिए कि f(x)=1x द्वारा परिभाषित फलन f:R∗→R∗ एकैकी तथा आच्छादक है, जहाँ R∗ सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है । यदि प्रांत R∗ को N से बदल दिया जाए , जबकि सहप्रांत पूर्ववत R∗ ही रहे , तो भी क्या यह परिणाम सत्य होगा ?
View Solutionमान लीजिए कि f:{1,3,4}→{1,2,5} तथा g:{1,2,5}→{1,3},f={(1,2),(3,5),(4,1)} तथा g={(1,3),(2,3),(5,1)} द्वारा प्रदत्त हैं । gof ज्ञात कीजिए ।
View Solutionएक सम्बन्ध R={(x,y):x,y∈A औरx<y} समुच्चय A={1,2,3,4,5} पर परिभाषित है, सम्बन्ध R है -
View Solutionदिए हुए वक्रो एव रेखाओ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए :
(i) y=x2,x=1,x=2 एव X - अक्ष
(ii) y=x4,x=1,x=5 एव X - अक्ष
View Solutionसिद्ध कीजिए कि सारणिक ∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣,θ से स्वतंत्र है।
View Solutionसिद्ध कीजिए कि समस्त त्रिभुजो के समुच्यो A मै R={(T1,T2):T1,T2 के समरूप है। द्वारा परिभाषित संबंध R एक तुलयता संबंध है। भुजाओ 3, 4, 5 वाले समकोण त्रिभुज T1 भुजाओ 5, 12, 13 वाले समकोण त्रिभुज T2, तथा भुजाओं 6, 8 10 वाले सगकोण त्रिभुज T3 पर विचार कीजिए। T1,T2औरT3, में से कौन से त्रिभुज परस्पर संबंधित है?
View Solutionसिद्ध कीजिये की समस्त त्रिभुजों के समुच्चय A में, R={T1,T2}:T1,T2 के समरूप है, द्वारा परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T3 पर विचार कीजिये। T1,T2 और T3 में से कौन से त्रिभुज परस्पर संबंधित हैं?
View SolutionFind the sum of first 24 terms of on AP t1,t2,t3,...., if it is known that t1+t5+t10+t15+t20+t24=225.
View SolutionIf the sequence t1,t2,t3,… are in A.P. then the sequence t6,t12,t18,… is
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
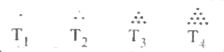
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View Solution