ऐसे सम्बन्ध का उदाहरण दीजिये, जो
(i) सममित हो परन्तु न तो स्वतुल्य हो और न संक्रमक हो ।
(ii) संक्रमक हो परन्तु न तो स्वतुल्य हो और न सममित हो ।
(iii) स्वतुल्य तथा सममित हो किन्तु सममित न हो ।
(iv) स्वतुल्य तथा संक्रमक हो किन्तु सममित न हो ।
(v) सममित तथा संक्रमक हो किन्तु स्वतुल्य न हो ।
(i) माना समुच्चय A={1,2,3}
तथा सम्बन्ध R={(1,2),(2,1)}A पर परिभाषित है ।
:'(1,1)cancelin R
∴R स्वतुल्य नहीं है ।
∵(1,2)∈R⇒(2,1)∈R
∴R सममित है ।
∵(1,2)∈R तथा (2,1) in R rArr(1,1) cancelin R
∴R संक्रमक नहीं है ।
(ii) माना वास्तविक संख्याओं के समुच्चय R पर परिभाषित सम्बन्ध S={(a,b):a<b} है ।
प्रत्येक a∈Rके लिये,(a,a) cancelin S क्योंकि a<aअसत्य है ।
∴S स्वतुल्य नहीं है
प्रत्येक a,b∈R के लिए,
माना (a,b)∈S⇒a<b
cancelrArr b lt a
cancelrArr (b,a) in S
∴S सममित नहीं है ।
प्रत्येक a,b,c∈R के लिये
माना (a,b)∈S तथा (b,c)∈S
⇒a<b तथा b<c⇒a<c⇒(a,c)∈S
∴Sसंक्रमक है ।
(iii) माना A={1,2,3} के समुच्चय पर परिभाषित सम्बन्ध
R={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2)} है ।
∵ प्रत्येक a∈A के लिये(a,a)∈R
∴R स्वतुल्य है ।
प्रत्येक (a,b) in R cancelin (a,c) in R
∴R सममित है ।
प्रत्येक (a,b)∈R तथा (b,c) in R cancelrArr (a,c) in R
∴R संक्रमक नहीं है ।
(:'(1,2)in R, (2,3) in R "परन्तु" (1,3) cancelin R)
(iv) वास्तविक संख्याओं के समुच्चय पर परिभाषित सम्बन्ध
R={(a,b):a3≥b3} है ।
प्रत्येक a∈Rके लिये (a,a)∈R
∴R एक स्वतुल्य है ।
यदि (2,1)∈R⇒23>13
cancelrArr 1^(3) gt 2^(3)
cancelrArr (1,2) in R
∴R सममित नहीं है ।
तथा प्रत्येक (a,b)∈Rतथा (b,c)∈R
⇒a3≥b3 तथा b3≥c3
⇒a3≥c3
⇒(a,c)∈R
∴Rसंक्रमक है ।
(v) समुच्चय A={1,2,3} पर परिभाषित सम्बन्ध
R={(1,1),(2,2),(1,2),(2,1)}है ।
:' (3,3)cancelin R
∴R स्वतुल्य नहीं है ।
प्रत्येक (a,b)∈R⇒(b,a)∈R
∴Rसममित है ।
प्रत्येक (a,b)∈Rतथा (b,c)∈R
⇒(a,c)∈R
∴Rसंक्रमक है ।
Topper's Solved these Questions
- सम्बन्ध एवं फलन BOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलन EXERCISE - एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.2))
12 Videos
- सम्बन्ध एवं फलन BOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलन EXERCISE - एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.3))
14 Videos
- सम्बन्ध एवं फलन BOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलन EXERCISE - प्रश्नावली (1E) (विविध प्रतियोगी परीक्षाओं हेतु प्रश्न )
10 Videos
- समाकलनो के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - समाकलनो के अनुप्रयोग EXERCISE - विविध प्रश्नवली
19 Videos
- सारणिकBOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - विविध प्रश्नावली
19 Videos
Similar Questions
सिद्ध कीजिए कि f(x)=1x द्वारा परिभाषित फलन f:R∗→R∗ एकैकी तथा आच्छादक है, जहाँ R∗ सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है । यदि प्रांत R∗ को N से बदल दिया जाए , जबकि सहप्रांत पूर्ववत R∗ ही रहे , तो भी क्या यह परिणाम सत्य होगा ?
View Solutionमान लीजिए कि f:{1,3,4}→{1,2,5} तथा g:{1,2,5}→{1,3},f={(1,2),(3,5),(4,1)} तथा g={(1,3),(2,3),(5,1)} द्वारा प्रदत्त हैं । gof ज्ञात कीजिए ।
View Solutionएक सम्बन्ध R={(x,y):x,y∈A औरx<y} समुच्चय A={1,2,3,4,5} पर परिभाषित है, सम्बन्ध R है -
View Solutionदिए हुए वक्रो एव रेखाओ से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए :
(i) y=x2,x=1,x=2 एव X - अक्ष
(ii) y=x4,x=1,x=5 एव X - अक्ष
View Solutionसिद्ध कीजिए कि सारणिक ∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣,θ से स्वतंत्र है।
View Solutionयदि A सममित आव्यूह हो, तो सिद्ध करो कि M'AM भी सममित आव्यूह होगा|
View Solutionयदि A तथा B व्यत्क्रमणीय हो, तो
View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि कोई ऐसे बिंदु निश्चित करना संभव न हो, जहाँ समस्या का अनुकूलतम हल हो, तो समस्या का हल अपरिवद्ध होता है।
View Solutionप्रतिशतता ज्ञात करना सीखें जबकि योग सौ न हो
View Solutionयदि a,b का माध्य 8 हो और a, b,c का माध्य भी 8 हो, तो ज्ञात कीजिए।
View Solutionमैं कगारे का वृक्ष हो रहा हूँ, न मालूम कब गिर पहूँ। ये शब्द किसके हैं?
View Solutionउदाहरण |संबंधों के प्रकार |रिक्त संबंध |सार्वत्रिक संबंध|तत्समक संबंध |स्वतुल्य संबंध |सममित संबंध |संक्रमक संबंध |OMR
View Solutionयदि + का अर्थ ÷, × का अर्थ - हो, - का अर्थ × और ÷ का अर्थ + हो, तो 38+19-16×17÷3=?
View Solutionमेरे बड़े भाई साहब मुझसे पाँच साल बड़े थे, लेकिन केवल तीन दरजे आगे। उन्होंने भी उसी उम्र में पढ़ना शुरू किया था, जब मैंने शुरू किया, लेकिन तालीम जैसे महत्त्वपूर्ण मामले में वह जल्दबाजी से काम लेना पसंद नहीं करते थे, इस भवन की बुनियाद खूब मज़बूत डालना चाहते थे, जिस पर आलीशान महल बन सके। एक साल का काम दो साल में करते थे। कभी-कभी तीन साल भी लग जाते थे। बुनियाद ही पुखता न हो तो मकान कैसे पायेदार बने।
मैं छोटा था, वह बड़े थे। मेरी उम्र नौ साल की थी, वे चौदह साल के थे। उन्हें मेरी निगरानी का पूरा और जन्मसिद्ध अधिकार था। और मेरी शालीनता इस बात में थी कि मैं उनके हुक्म को कानून समझू। वह स्वभाव के बड़े अध्ययनशील थे। हरदम किताब खोले बैठे रहते और शायद दिमाग को आराम देने के लिए कभी कॉपी पर, कभी किताब के हाशियों पर, चिड़ियो, कुत्तों, बिल्लियों की डालते थे। कभी एक ही शायरी को बार-बार सुंदर अक्षरों में नकल करते थे। कभी ऐसी शब्द-रचना करते जिसमें न कोई अर्थ होता, न कोई सामंजस्य। जैसे एक बार उनकी कॉपी पर मैंने इबारत देखी-स्पेशल, अमीना, भाइयों-भाईयो, भाई-भाई, श्रीयुत् राधेश्याम--इनके बाद आदमी का चेहरा बना हुआ था। मैंने बहुत चेष्टा की कि इस पहेली का कोई हल निकालूँ, लेकिन असफल रहा ओर उनसे पूछने का साहस न हुआ। वे नवीं कक्षा में थे, मैं पाँचवी में। उनकी रचनाओं को समझना मेरे लिए छोटा मुँह और बड़ी बात थी।
"युनियाद ही पुख्ता न हो तो मकान कैसे पायदार बने" छोटे भाई के उक्त कथन में निहित है
View Solutionक्रमचय , जब सभी वस्तुएं भिन्न न हो
View Solutionदो परमाणु X और Y अध्रुवीय और विद्युत् सममित हैं।
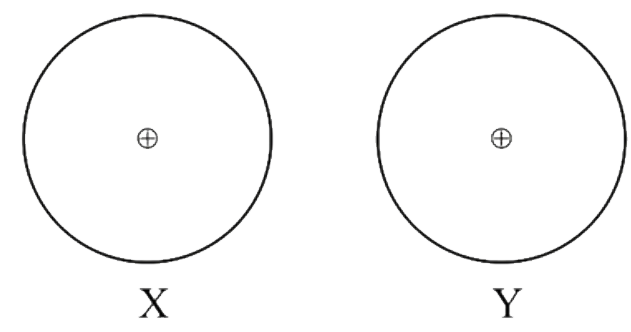
उनके मध्य किस प्रकार का अंतरा अणुक आकर्षण बल विकसित हो सकता है ?
View Solution
