बहुपद x4+x3−34x2−4x+120 के सभी मूल ज्ञात कीजिये यदि इसके दो मूल 2 और -2 है |
माना कि, f(x)=x4+x3−34x2−4x+120
चूँकि f(x) के दो मूल 2 और -2 है |
⇒(x+2) और (x−2),f(x) के गुणनखण्ड है |
⇒(x+2)⋅(x−2),f(x) का एक गुणनखण्ड है |
⇒(x2−4),f(x) का एक गुणनखण्ड है |
अब f(x) को x2−4 से विभाजित करने पर,
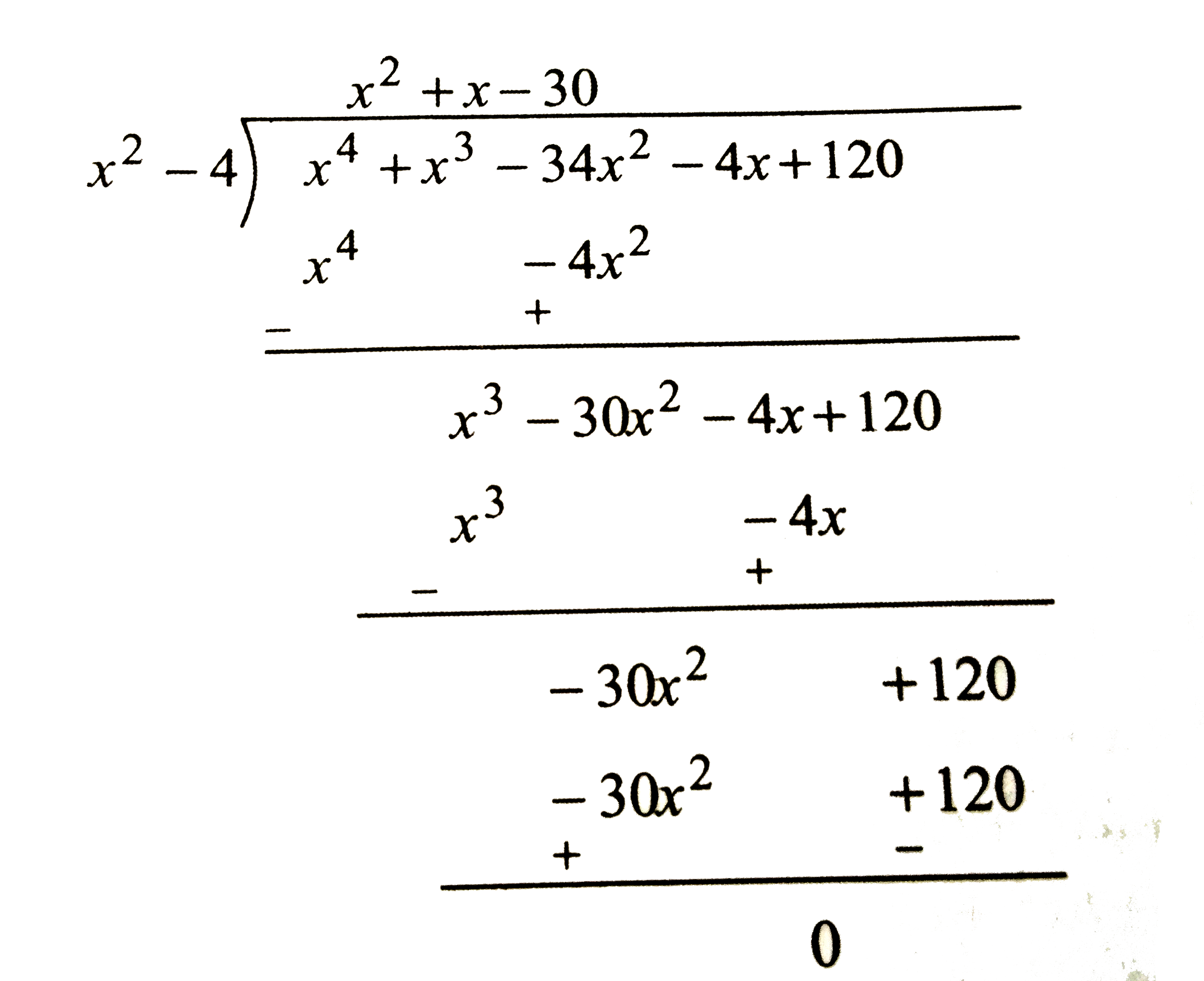
स्पष्टतः अन्य गुणनखण्ड x2+x−30 जिसके मूल है x2+x−30=0
⇒(x+6)(x−5)=0
⇒x=5,−6
अतः f(x) के सभी मूल 2,−2,5 और -6 है |
Topper's Solved these Questions
- बहुपदBOOK - BALAJI PUBLICATIONCHAPTER - बहुपदEXERCISE - अध्याय प्रश्न 2.1
24 Videos
- बहुपदBOOK - BALAJI PUBLICATIONCHAPTER - बहुपदEXERCISE - अध्याय प्रश्न 2.2
30 Videos
- प्रायिकता BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता EXERCISE - स्वमूल्यांकन परीक्षण
19 Videos
- रचनाऐBOOK - BALAJI PUBLICATIONCHAPTER - रचनाऐEXERCISE - स्वमूल्यांकन परिक्षण
2 Videos
Similar Questions
यदि बहुपद x2+x+1 के मूल α और β है तब α+β का मान ज्ञात कीजिये |
View Solutionयदि α,β,γ बहुपद 2x3+x2−13x+16 के मूल है , तब αβγ का मान ज्ञात कीजिये |
View Solutionएक पिग्गी बैंक में 50 पैसे के 100 सिक्के है, 1 रूपये के 50 सिक्के है, 2 रूपये के 20 सिक्के है और 5 रूपये के 20 सिक्के है। यदि पिग्गी बैंक को हिलाकर उल्टा करने पर कोई एक सिक्का गिरने के परिणाम सम्प्रायिक है तो इसकी क्या प्रायिकता है की वह गिरा हुआ सिक्का -
(i) 50 पैसे का होगा,
(ii) 5 रूपये का नहीं होगा?
View Solution5.6 सेमी का रेखाखण्ड खींचकर उसे 5:8 के अनुपात में अन्तः विभक्त कीजिए
View Solutionयदि बहुपद x4+x3−11x2−9x+18 के दो शून्यक 1 और -2 है तो इसके अन्य दो शून्यक ज्ञात कीजिए ।
View Solutionx=2 और x=3, समीकरण 3x^2-x-10 =0 के एक-दूसरे मूल है
View Solutionसरल रेखा x−12=y−21=z+3−3 के समांतर उस रेखा के समीकरण ज्ञात कीजिए जो मूल बिंदु से होकर जाती है।
View Solutionएक आयत की भुजाएँ x=2,x=−4,y=3 और y=−5 है। इसके विकर्णों के समीकरण ज्ञात कीजिए ।
View Solutionदो बहुपदो का लघुतम समापवर्तक x3−6x2+3x+10 है तथा महत्तम समापवर्तक (x+1) है। यदि एक बहुपद x2−4x−5 है तो दूसरा बहुपद ज्ञात कीजिये।
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionयदि समीकरण x2+px+q=0 के मूल, α,β है और समीकरण x2−rx+s=0 के मूल α4,β4 है, तो समीकरण x2−4qx+2q2−r=0 के सदैव
View Solutionयदि समीकरण x3−3x+2=0 के दो मूल बराबर हो, तो मूल होंगे।
View Solutionयदि a,b,c∈Q तो समीकरण (b+c−2a)x2+(c+a−2b)x+(a+b−2c)=0 के मूल है
View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
View Solutionयदि समीकरण x2−px+q=0 के मूल secα व cosecα है, तब
View Solutionयदि समीकरण (a2+4a+3)x2+(a2−a−2)x+a(a+1)=0 के दो से अधिक मूल हैं, तो a का मान है
View Solution
