माना त्रिभुज ABC का केन्द्रक G है|तब सिद्ध कीजिये की
AB2+BC2+CA2=3(GA2+GB2+GC2)
चित्र से माना A के निर्देशांक (x1,y1 ) है तब ΔABC के केन्द्रक G के निर्देशांक निम्न होंगें|
(0+a+x13,0+0+y13)=(x1+a3,y13)
इसलिए AB2=(x1−0)2+(y1−0)2 ltbr gt =x21+y21
BC2p=(a−0)2+(0−0)2=a2
CA2=(x1−a)2+(y1−0)2
=(x1−a)2+y21
अतः AB2+BC2+CA2=(x21+y21)+a2+[(x1−a)2+y21]
=x21+y21+a2+x21+a2−2ax1+y21
तथा GA2=(x1+a3−x1)2+(y13−y1)2=19[(a−2x1)2+4y21]
GB2=(x1+a3−0)2+(y13−0)2=19[(x1+a)2+y21]
व GC2=(x1+a3−a)2+(y13−0)2=19[(x1+a)2+y21]
इसलिए 9(GA∘+GB2+GC2)
=[{(a−2x1)2+(x1+a)2+(x1−2a)2}+(4y21+y21+y21)]
=6(x21+a2−ax1+y21)
समीकरण (1 ) व (2 )से
AB2+BC2+CA2=3(GA2+GB2+GC2)
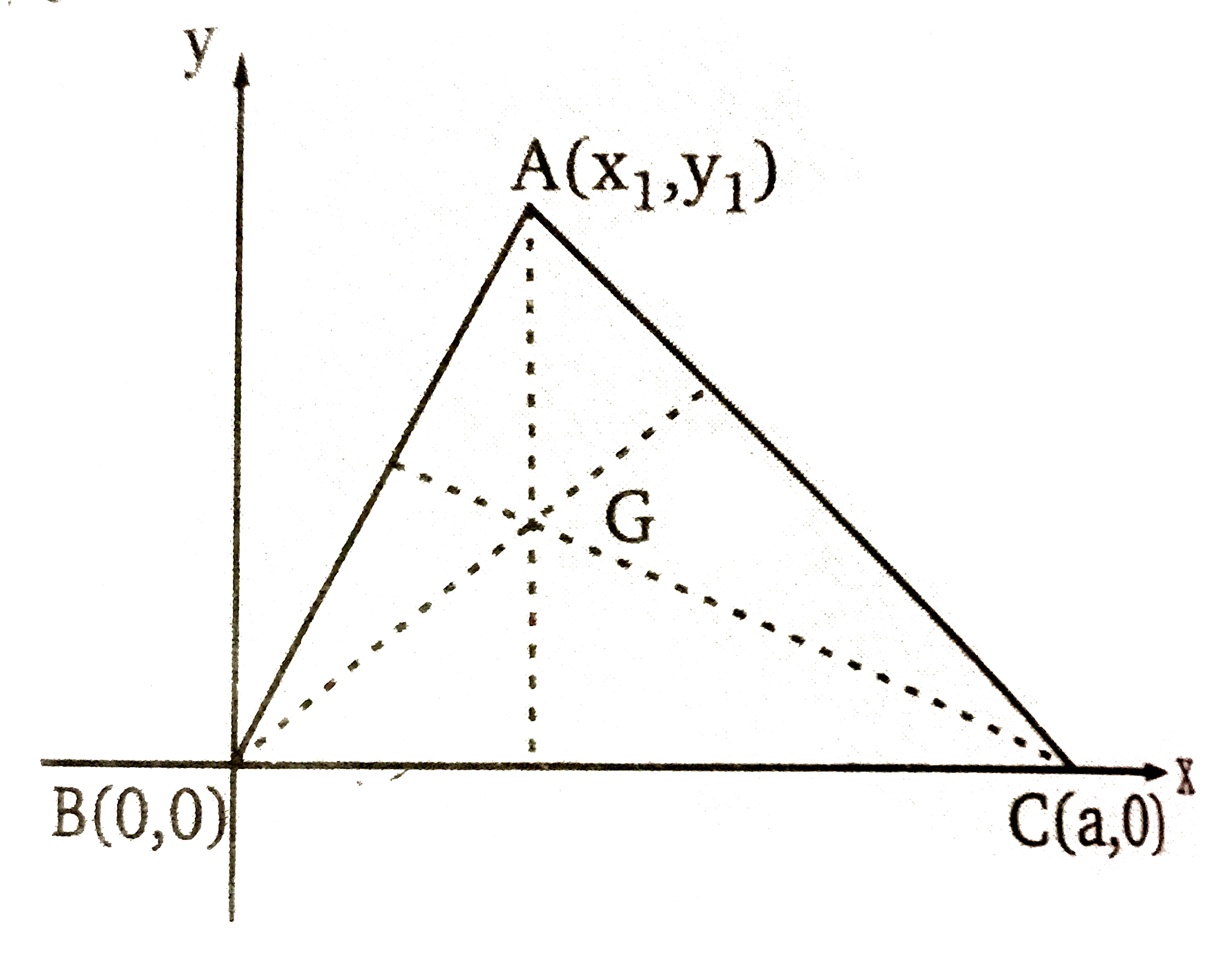
Topper's Solved these Questions
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास प्रश्न 6.1
6 Videos
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - अभ्यास प्रश्न 6.2 (अतिलघु उत्तरीय प्रश्न)
11 Videos
- द्विघात समीकरण BOOK - BALAJI PUBLICATIONCHAPTER - द्विघात समीकरण EXERCISE - स्वमूल्यांकन परिक्षण
31 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - स्वमूल्यांकन परीक्षण
23 Videos
Similar Questions
वह चतुर्थांश ज्ञात कीजिये जिसमें निम्न बिंदु स्थित है|
(i)(−1,−4) (ii)(4,1) (iii)(3,−2) (iv)(−3,1) (v)(7,2) (vi)(−3,−2) (vii)(−6,4) (viii)(2,−2)
View Solutionकिसी बिंदु का भुज किस चतुर्थांश में ऋणात्मक होता है?
View Solutionद्विघात समीकरण √3x2+10x−8√3=0 को हल कीजिए।
View Solution11 सेमी × 10 सेमी × 7 सेमी विमाओं वाला घनाभ बनाने के लिए 1.75 सेमी व्यास तथा 2 मिमी की मोटाई के कितने सिक्के पिघलाने पड़ेगें ?
View SolutionIf G be the centroid of the Delta ABC, then prove that AB^(2)+BC^(2)+CA^(2)=3(GA^(2)+GB^(2)+GC^(2))
View SolutionIf G be the centroid of a triangle ABC and P be any other point in the plane prove that PA^(2)+PB^(2)+PC^(2)=GA^(2)+GB^(2)+GC^(2)+3GP^(2)
View SolutionIf G be the centroid of a triangle ABC, prove that, AB2+BC2+CA2=3(GA2+GB2+GC2)
View SolutionABCD is a tetrahedron and G is the centroid of the base BCD.Prove that AB^(2)+AC^(2)+AD^(2)=GB^(2)+GC^(2)+GD^(2)+3GA^(2)
View SolutionLet a=BC,b=CA,C=AB be the sides of the triangle ABC.If G is the centroid of Delta ABC such that GB and GC and bar(GC) are inclined at an obtuse angle,then
View SolutionIf G be the centroid of the ΔABCandO be any other point in theplane of the triangle ABC, then prove that: OA2+OB2+OC2=GA2+GB2+GB2+GC2+3GO2
View SolutionIf G is the centroid of triangle with vertices A(a,0),B(−1,0) and C(b,c) then AB2+BC2+CA2GA2+GB2+GC2=
View SolutionIf G is the centroid of a ΔABC, then GA2+GB2+GC2 is equal to
View Solutionयदि G,ΔABC का केन्द्रक है और O,ΔABC के तल में कोई दूसरा बिन्दु है | तब सिध्द करे की OA2+OB2+OC2=GA2+GB2+GC2+3GO2
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solution∣∣ ∣ ∣∣a2+x2abcaabb2+x2bccabcc2+x3∣∣ ∣ ∣∣= का भाजक है
View Solution